题目内容
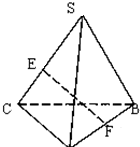 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:如图所示,取SA的中点M,连接ME,MF.又E,F分别是SC和AB的中点,利用数量积的中位线定理可得:ME∥AC,MF∥SB,ME=
AC=1,MF=
SB=1.又SB⊥AC,可得EM⊥FM.在Rt△EFM中,利用勾股定理即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:如图所示,取SA的中点M,连接ME,MF.
又∵E,F分别是SC和AB的中点,
∴ME∥AC,MF∥SB,ME=
AC=1,MF=
SB=1.
又SB⊥AC,∴EM⊥FM.
在Rt△EFM中,EF=
=
.
故选:A.

又∵E,F分别是SC和AB的中点,
∴ME∥AC,MF∥SB,ME=
| 1 |
| 2 |
| 1 |
| 2 |
又SB⊥AC,∴EM⊥FM.
在Rt△EFM中,EF=
| EM2+FM2 |
| 2 |
故选:A.
点评:本题考查了三角形的中位线定理、异面直线所成的角、勾股定理,考查了推理能力,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
定义在(-1,1)上的奇函数f(x)=
是奇函数,则常数m,n的值分别为( )
| x+m |
| x2+nx+1 |
| A、m=0,n=1 |
| B、m=1,n=1 |
| C、m=0,n=0 |
| D、m=1,n=1 |
不等式
≤0的解集为( )
| x+1 |
| 2x-1 |
A、(-∞,-
| ||
B、[-
| ||
C、(-∞,-1)∪[
| ||
D、[-1,
|
函数y=
的值域为( )
| 2x2+4x-7 |
| x2+2x+3 |
A、[-
| ||
B、(-
| ||
C、[-
| ||
D、[-
|
命题“存在x0∈R,2x0≤0”的否定是( )
| A、不存在x0∈R,2x0>0 |
| B、对任意的x∈R,2x>0 |
| C、对任意的x∈R,2x≤0 |
| D、存在x0∈R,2x0≥0 |
设f(x)=x8-x5+x2-x+1,则以下说法正确的是( )
| A、当x>0,f(x)≤0 |
| B、?x∈R,f(x)<0 |
| C、?x∈R,f(x)>0 |
| D、以上均不正确 |