题目内容
定义在(-1,1)上的奇函数f(x)=
是奇函数,则常数m,n的值分别为( )
| x+m |
| x2+nx+1 |
| A、m=0,n=1 |
| B、m=1,n=1 |
| C、m=0,n=0 |
| D、m=1,n=1 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由f(x)=
是定义在(-1,1)上的奇函数,得f(0)=0,由此求得m的值,结合f(-
)+f(
)=0求得n的值.
| x+m |
| x2+nx+1 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵f(x)=
是定义在(-1,1)上的奇函数,
∴f(0)=m=0,
则f(x)=
,再由f(-
)+f(
)=0得
+
=0,解得n=0.
∴常数m,n的值分别为0,0.
故选:C.
| x+m |
| x2+nx+1 |
∴f(0)=m=0,
则f(x)=
| x |
| x2+nx+1 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| ||||
(-
|
| ||||
(
|
∴常数m,n的值分别为0,0.
故选:C.
点评:本题考查了函数奇偶性的性质,定义在实数集上的奇函数,一定有f(0)=0,是基础题.

练习册系列答案
相关题目
函数f(x)=|x2-2|-lgx的零点个数有( )个.
| A、1 | B、2 | C、3 | D、无数个 |
定义:若z2=a+bi(a,b∈R,i为虚数单位),则称复数z是复数a+bi的平方根.根据定义,则复数-3+4i的平方根是( )
| A、1-2i或-1+2i |
| B、1+2i或-1-2i |
| C、-7-24i |
| D、7+24i |
已知f′(2)=2,f(2)=3,则
+1的值为( )
| lim |
| x→2 |
| f(x)-3 |
| x-2 |
| A、1 | B、2 | C、3 | D、4 |
设f(x)是定义在实数集R上的奇函数,且满足f(x+2)=-f(x),当0≤x≤1时,有f(x)=x,则f(7.5)=( )
| A、7.5 | B、1.5 |
| C、0.5 | D、-0.5 |
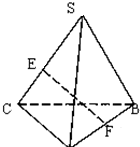 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
 如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证:
如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证: