题目内容
设x1、x2 是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点,且|x1|+|x2|=2
,则b的最大值为 .
| 2 |
考点:利用导数研究函数的极值
专题:综合题,导数的概念及应用
分析:先对函数进行求导,根据函数f(x)=ax3+bx2-a2x(a>0)的两个极值点为x1,x2(x1≠x2),可以得到△>0且由韦达定理可得x1+x2,x1x2,把等式转化为关于x1+x2,x1x2的关系式,求出a、b的关系,把a看成未知数x,求三次函数的最值,利用导数求极值,是b2最大值,开方可求b的最大值.
解答:
解:∵f(x)=ax3+bx2-a2x(a>0),
∴f′(x)=3ax2+2bx-a2(a>0),
∵函数f(x)=ax3+bx2-a2x(a>0)的两个极值点为x1,x2(x1≠x2),
∴f'(x)=0有两不等实根x1,x2(x1≠x2),
∴△>0,∴b2+3a3>0,恒成立,
∴x1+x2=-
,x1x2=-
<0,
∵|x1|+|x2|=2
,且x1,x2异号,
∴(|x1|+|x2|)2=x12+x22-2x1x2=(x1+x2)2-4x1x2=8,
∴(-
)2+
=8,∴b2=-3a3+18a2≥0,解得0<a≤6,
设t=-3a3+18a2,则t′=-9a2+36a=-9a(a-4)(0<a≤6),
令t′>0,得0<a<4,t′<0,得6≥a>4,
t在(0,4]是增函数,在[4,6)是减函数,
∴a=4取得t最大96,∴b2最大值为96,∴bmax=4
故答案为:4
.
∴f′(x)=3ax2+2bx-a2(a>0),
∵函数f(x)=ax3+bx2-a2x(a>0)的两个极值点为x1,x2(x1≠x2),
∴f'(x)=0有两不等实根x1,x2(x1≠x2),
∴△>0,∴b2+3a3>0,恒成立,
∴x1+x2=-
| 2b |
| 3a |
| a |
| 3 |
∵|x1|+|x2|=2
| 2 |
∴(|x1|+|x2|)2=x12+x22-2x1x2=(x1+x2)2-4x1x2=8,
∴(-
| 2b |
| 3a |
| 4a |
| 3 |
设t=-3a3+18a2,则t′=-9a2+36a=-9a(a-4)(0<a≤6),
令t′>0,得0<a<4,t′<0,得6≥a>4,
t在(0,4]是增函数,在[4,6)是减函数,
∴a=4取得t最大96,∴b2最大值为96,∴bmax=4
| 6 |
故答案为:4
| 6 |
点评:由原函数极值点的个数判断出导函数解的个数,利用判别式得参数的关系,用韦达定理把参数和解联系起来,韦达定理是个很好的“桥梁”,求最大值要先求极大值,三次函数一般用导数来求.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
函数f(x)=|x2-2|-lgx的零点个数有( )个.
| A、1 | B、2 | C、3 | D、无数个 |
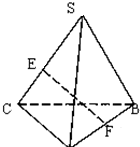 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|