题目内容
(Ⅰ)计算题,求[125
+(
) -
+343
]
+(
)0-ln
;
(Ⅱ)解方程:lg(10x)+2=4lgx.
| 2 |
| 3 |
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| e |
(Ⅱ)解方程:lg(10x)+2=4lgx.
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(Ⅰ)利用指数和对数的运算法则和运算性质求解.
(Ⅱ)由已知得3lgx=3,由此能求出x=10.
(Ⅱ)由已知得3lgx=3,由此能求出x=10.
解答:
解:(Ⅰ)[125
+(
) -
+343
]
+(
)0-ln
=(25+4+7)
+1-
=6+
=
.
(Ⅱ)∵lg(10x)+2=4lgx,
∴1+lgx+2=4lgx,
∴3lgx=3,
解得x=10.
| 2 |
| 3 |
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| e |
=(25+4+7)
| 1 |
| 2 |
| 1 |
| 2 |
=6+
| 1 |
| 2 |
=
| 13 |
| 2 |
(Ⅱ)∵lg(10x)+2=4lgx,
∴1+lgx+2=4lgx,
∴3lgx=3,
解得x=10.
点评:本题考查指数式的运算,考查对数方程的求解,是基础题,解题时要注意指数和对数的运算法则和运算性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
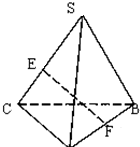 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
 如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证:
如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证: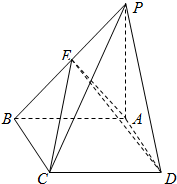 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点.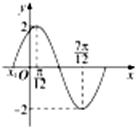 已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.