题目内容
函数y=
的值域为（ ）
| 2x2+4x-7 |
| x2+2x+3 |
A、[-
| ||
B、（-
| ||
C、[-
| ||
D、[-
|
考点：函数的值域
专题：函数的性质及应用
分析：利用判别式法求函数的值域．
解答：
解：∵y=
，
∴（y-2）x2+（2y-4）x+3y+7=0，
当y-2≠0时，△=（2y-4）2-4（y-2）（3y+7）≥0，
解得-
≤y＜2．
当y=2时，2x2+4x+6=2x2+4x-7不成立，
∴函数y=
的值域为[-
，2）．
故选：D．
| 2x2+4x-7 |
| x2+2x+3 |
∴（y-2）x2+（2y-4）x+3y+7=0，
当y-2≠0时，△=（2y-4）2-4（y-2）（3y+7）≥0，
解得-
| 9 |
| 2 |
当y=2时，2x2+4x+6=2x2+4x-7不成立，
∴函数y=
| 2x2+4x-7 |
| x2+2x+3 |
| 9 |
| 2 |
故选：D．
点评：本题考查函数的值域的求法，是基础题，解题时要注意函数的性质的合理运用．
练习册系列答案
相关题目
定义：若z2=a+bi（a，b∈R，i为虚数单位），则称复数z是复数a+bi的平方根．根据定义，则复数-3+4i的平方根是（ ）
| A、1-2i或-1+2i |
| B、1+2i或-1-2i |
| C、-7-24i |
| D、7+24i |
设f（x）是定义在实数集R上的奇函数，且满足f（x+2）=-f（x），当0≤x≤1时，有f（x）=x，则f（7.5）=（ ）
| A、7.5 | B、1.5 |
| C、0.5 | D、-0.5 |
已知集合M={y|y＞1}，N={y|y=x2，x∈R}，则M∩N=（ ）
| A、（0，+∞） |
| B、[0，+∞） |
| C、（1，+∞） |
| D、[1，+∞） |
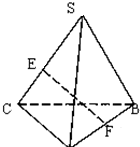如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E，F分别是SC和AB的中点，则EF的长是（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
把一颗骰子投掷两次，第一次出现的点数记为m，第二次出现的点数记为n，方程组
只有一组解的概率是（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
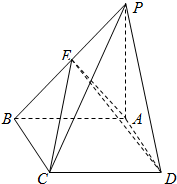如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，且PA=AB=1，F为PB中点．