题目内容
已知f（x）=2sin（x+
），x∈R．
（1）求f（
）的值；
（2）设α，β∈∈[0，
]，f（α）=2，f（β）=
，求f（α+β）的值．
| π |
| 6 |
（1）求f（
| π |
| 6 |
（2）设α，β∈∈[0，
| π |
| 3 |
| 8 |
| 5 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：（1）直接根据函数f（x）的解析式求得f（
）的值．
（2）根据f（α）=2，求得sin（x+
）的值，可得α的值．根据 f（β）=
，求得sin（β+
）的值，可得cos（β+
）的值．再根据f（α+β）=2sin（α+β+
）=2cosβ=2cos[（β+
）-
]，利用两角和差的余弦公式求得f（α+β）的值．
| π |
| 6 |
（2）根据f（α）=2，求得sin（x+
| π |
| 6 |
| 8 |
| 5 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答：
解：（1）f（
）=2sin（
+
）=2sin
=
．
（2）∵α，β∈[0，
]，f（α）=2sin（α+
）=2，∴sin（α+
）=1，
∴α+
=
，α=
．
∵f（β）=2sin（β+
）=
，∴sin（β+
）=
，
∵β+
∈[
，
]，∴cos（β+
）=
．
∴f（α+β）=2sin（α+β+
）=2sin（
+β）=2cosβ
=2cos[（β+
）-
]=2cos（β+
）cos
+2sin（β+
）sin
=2×
×
+2×
×
=
．
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 3 |
（2）∵α，β∈[0，
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
∴α+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵f（β）=2sin（β+
| π |
| 6 |
| 8 |
| 5 |
| π |
| 6 |
| 4 |
| 5 |
∵β+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
∴f（α+β）=2sin（α+β+
| π |
| 6 |
| π |
| 2 |
=2cos[（β+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=2×
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
3
| ||
| 5 |
点评：本题主要考查同角三角函数的基本关系、两角和差的正弦公式的应用，属于中档题．
练习册系列答案
相关题目
函数f（x）=2sin（2x-φ）（|φ|＜
）的图象如图所示，则φ的值等于（ ）
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若向量
=（2，-1），
=（0，2），则以下向量中与
+
垂直的是（ ）
| a |
| b |
| a |
| b |
| A、（1，-2） |
| B、（1，2） |
| C、（2，1） |
| D、（0，2） |
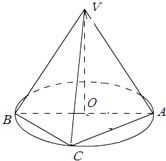如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，已知AB=2，VA=VB=VC=2．