题目内容
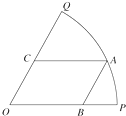 地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=
地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=| π |
| 3 |
考点:在实际问题中建立三角函数模型
专题:解三角形
分析:过点B作BM⊥OP于M,则BM=sinα,OM=cosα,建立面积与角α的三角函数式,然后变形利用三角函数的公式以及最值求S的最大值.
解答:
解:过点B作BM⊥OP于M,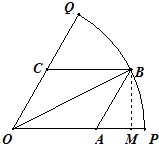
则BM=sinα,OM=cosα,OA=OM-AM=cosα-
sinα,设平行四边形OABC的面积为S,
则S=OA•BM=(cosα-
sinα)sinα
=
sin2α-
sin2α
=
sin2α+
cos2α-
=
(
sin2α+
cos2α)-
=
sin(2α+
)-
,
因为0<α<
,所以2α+
=
,即α=
时,Smax=
-
=
;
所以当A是
的中点时,能使裁下的钢板面积最大,最大面积为
.

则BM=sinα,OM=cosα,OA=OM-AM=cosα-
| ||
| 3 |
则S=OA•BM=(cosα-
| ||
| 3 |
=
| 1 |
| 2 |
| ||
| 3 |
=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 6 |
=
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
=
| ||
| 3 |
| π |
| 6 |
| ||
| 6 |
因为0<α<
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |
所以当A是
 |
| PQ |
| ||
| 6 |
点评:本题考查了两角和与差的三角函数的运用以及倍角公式、三角函数的最值等知识的综合应用.

练习册系列答案
相关题目
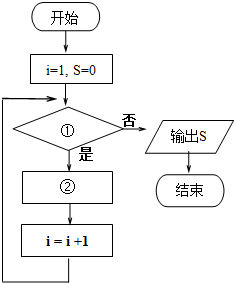 已知等比数列{an}中,a1=1,公比q=2,计算数列{an}的前20项的和S,现已给出该算法的程序框图如图所示:
已知等比数列{an}中,a1=1,公比q=2,计算数列{an}的前20项的和S,现已给出该算法的程序框图如图所示: