题目内容
已知点集P={（x，y）|1≤x≤4，1≤y≤3，x，y∈Z}，从P中选出四个不同的点组成平行四边形，求：
（1）其中一组对边与x轴平行的平行四边形有多少个？
（2）所有平行四边形有多少个？
（1）其中一组对边与x轴平行的平行四边形有多少个？
（2）所有平行四边形有多少个？
考点：排列、组合的实际应用
专题：排列组合
分析：画出点的集合，再根据平行四边形的类型，分类讨论即可，再根据分类计数原理可得答案．
解答：
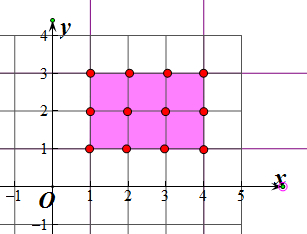解：点集P={（x，y）|1≤x≤4，1≤y≤3，x，y∈Z}，如图所示，
（1）第一类，（斜平行四边形）从其中一行中任选2个点，在从另外一行行中任选2个点距离和第一次选的点的距离一样，有3×2×（2+1+1）=24个，
第二类，（直平行四边形）从其中一行中任选2个点，在从另外一行行中对应的2个点，
有3×（3+2+1）=18个，
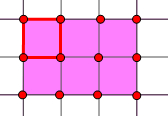
故根据分类计数原理，一组对边与x轴平行的平行四边形有24+18=42个，
（2）所有的平行四边形，
第一类，和x轴平行的有42个，
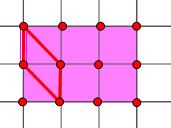
第二类，和y轴行，且不和x轴平行的有，2×3+2×2+2×1=12，
第二类，即不和x轴行也不和y轴平行，如图形式的平行四边形，有6个，
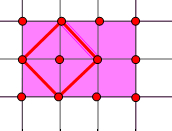
故共有42+12+6=60个，
解：点集P={（x，y）|1≤x≤4，1≤y≤3，x，y∈Z}，如图所示，（1）第一类，（斜平行四边形）从其中一行中任选2个点，在从另外一行行中任选2个点距离和第一次选的点的距离一样，有3×2×（2+1+1）=24个，
第二类，（直平行四边形）从其中一行中任选2个点，在从另外一行行中对应的2个点，
有3×（3+2+1）=18个，
故根据分类计数原理，一组对边与x轴平行的平行四边形有24+18=42个，
（2）所有的平行四边形，
第一类，和x轴平行的有42个，
第二类，和y轴行，且不和x轴平行的有，2×3+2×2+2×1=12，
第二类，即不和x轴行也不和y轴平行，如图形式的平行四边形，有6个，
故共有42+12+6=60个，
点评：本题主要考查了分类计数原理，如何分类是关键，属于中档题．
练习册系列答案
相关题目
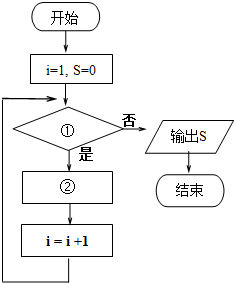已知等比数列{an}中，a1=1，公比q=2，计算数列{an}的前20项的和S，现已给出该算法的程序框图如图所示：
如图，在△ABC中，AD、BE分别是BC、AC边上的高，∠C=60°，求证：