题目内容
如图,在正方体ABCD-A1B1C1D1中,E、F分别为ABCD-A1B1C1D1、ABCD-A1B1C1D1的中点.
(1)求证:AC⊥BD1;
(2)AE∥平面BFD1.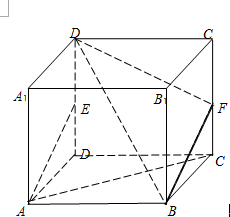
(1)求证:AC⊥BD1;
(2)AE∥平面BFD1.

考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)连接BD,交AC于0,通过证明AC⊥BD,DD1⊥AC利用线面垂直的判定定理证明出AC⊥平面BDD1,进而根据线面垂直的性质证明出AC⊥BD1.
(2)连接EF,构造出四边形ABEF并证明其为平行四边形,进而推断出AE∥BF,利用线面平行的判断定理证明出AE∥平面BFD1.
(2)连接EF,构造出四边形ABEF并证明其为平行四边形,进而推断出AE∥BF,利用线面平行的判断定理证明出AE∥平面BFD1.
解答:
(1)证明:连接BD,交AC于0,
∵DD1⊥平面ABCD,AC⊆平面ABCD,
∴DD1⊥AC,
∵ABCD为正方形,
∴AC⊥BD,
∵BD?平面BDD1,DD1?平面BDD1,BD∩DD1=D,
∴AC⊥平面BDD1,
∵BD1?平面BDD1,
∴AC⊥BD1.
(2)连接EF,
∵E,F为中点,
∴EF∥CD,且EF=CD,
∵AB∥CD,且AB=CD,
∴四边形ABEF为平行四边形,
∴AE∥BF,
∵BF?平面BFD1,AE?平面BFD1,
∴AE∥平面BFD1.
∵DD1⊥平面ABCD,AC⊆平面ABCD,
∴DD1⊥AC,
∵ABCD为正方形,
∴AC⊥BD,
∵BD?平面BDD1,DD1?平面BDD1,BD∩DD1=D,
∴AC⊥平面BDD1,
∵BD1?平面BDD1,
∴AC⊥BD1.
(2)连接EF,
∵E,F为中点,
∴EF∥CD,且EF=CD,
∵AB∥CD,且AB=CD,
∴四边形ABEF为平行四边形,
∴AE∥BF,
∵BF?平面BFD1,AE?平面BFD1,
∴AE∥平面BFD1.
点评:本题主要考查线面垂直和线面平行的判定定理的运用.注重了对学生基础知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
( )
| ex-e-x |
| 2 |
| A、是奇函数,它在R上是减函数 |
| B、是偶函数,它在R上是减函数 |
| C、是奇函数,它在R上是增函数 |
| D、是偶函数,它在R上是增函数 |
下列函数中,值域是{y|y≠0}的是( )
| A、y=x2+2x+3 | ||
| B、y=3x+6 | ||
C、y=
| ||
| D、y=loga(2x2-1) |
已知函数f(x)=
,则f(-2)=( )
|
| A、1 | B、2 | C、-1 | D、-2 |
 (1)说明由函数y=log3(x-1)作怎样的变换可以得到函数y=log3(x+2)的图象;
(1)说明由函数y=log3(x-1)作怎样的变换可以得到函数y=log3(x+2)的图象;