题目内容
20.已知函数y=$\frac{sinx}{x}$+$\sqrt{x}$+2,则y′=$\frac{xcosx-sinx}{{x}^{2}}+\frac{1}{2\sqrt{x}}$.分析 直接利用基本初等函数的求导公式及导数的运算法则求解.
解答 解:∵y=$\frac{sinx}{x}$+$\sqrt{x}$+2,
∴y′=$\frac{xcosx-sinx}{{x}^{2}}+\frac{1}{2}•{x}^{-\frac{1}{2}}$=$\frac{xcosx-sinx}{{x}^{2}}+\frac{1}{2\sqrt{x}}$,
故答案为:$\frac{xcosx-sinx}{{x}^{2}}+\frac{1}{2\sqrt{x}}$.
点评 本题考查导数的运算,考查了基本初等函数的求导公式,考查了导数的运算法则,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知圆C的标准方程为x2+y2=1,直线l的方程为y=k(x-2),若直线l和圆C有公共点,则实数k的取值范围是 ( )
| A. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | [-1,1] |
8.已知平面向量$\overrightarrow{a}$=(2,1),$\overrightarrow{c}$=(1,-1),若向量$\overrightarrow{b}$满足($\overrightarrow{a}$-$\overrightarrow{b}$)∥$\overrightarrow{c}$,($\overrightarrow{a}$+$\overrightarrow{c}$)⊥$\overrightarrow{b}$,则向量$\overrightarrow{b}$=( )
| A. | (2,1) | B. | (1,2) | C. | (3,0) | D. | (0,3) |
5.已知tanα=-$\frac{3}{4}$,且tan(α+β)=1,则tanβ的值为( )
| A. | -7 | B. | 7 | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
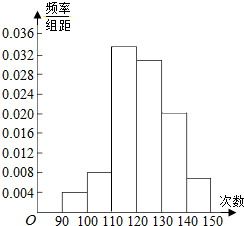 为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.
为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.