题目内容
10．
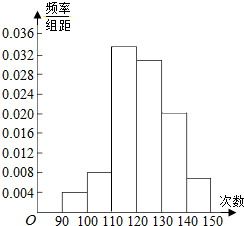为了了解高一学生的体能情况，某校抽取部分学生进行一部分跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12，若次数在110以上（含110次）为达标，试估计该学校全体高一学生单调达标率是0.88．
分析 根据从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12，用比值做出样本容量，根据样本容量和前两个小长方形所占的比例，用所有的样本容量减去前两个的频数之和，得到结果，除以样本容量得到概率．
解答 解：∵从左到右各小长方形的面积之比为2：4：17：15：9：3，
第二小组频数为12．
∴样本容量是$\frac{（2+4+17+15+9+3）×12}{4}$=150，
∵次数在110以上为达标，
次数在110以上的有150（1-$\frac{6}{50}$）=132，
∴全体高一学生的达标率为$\frac{132}{150}$=0.88．
点评 本题考查频率分步直方图的应用，是一个基础题，这种题目解题的关键是看清图中所给的条件，知道小长方形的面积就是这组数据的频率．
练习册系列答案
相关题目
4．已知角θ的终边经过点P（-x，-6），且cosθ=-$\frac{3}{5}$，则x=（ ）
| A． | $\frac{9}{2}$ | B． | -$\frac{9}{2}$ | C． | $\frac{2}{9}$ | D． | -$\frac{2}{9}$ |
1．集合{x∈N|-1＜x＜3}的真子集的个数是（ ）
| A． | 8 | B． | 7 | C． | 4 | D． | 3 |
5．已知p：m∈（-2，-1），q：m满足$\frac{x^2}{2+m}-\frac{y^2}{m+1}=1$表示椭圆，那么p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
2．已知角α的终边经过点（-6，8），则cosα=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{4}{5}$ |