��Ŀ����
12����֪����$f��x��=cos2x+\sqrt{3}sin2x$���������ĸ������У��ٺ����ı���ʽ���Ը�дΪ$f��x��=2cos��2x-\frac{��}{3}��$��
�ڵ�$x=k��+\frac{��}{6}$��k��Z��ʱ������ȡ�����ֵΪ2��
����x1��x2����f��x1��=f��x2��=0����${x_1}-{x_2}=\frac{k��}{2}��k��Z��k��0��$��
�ܺ���f��x����ͼ�����ֱ��$x=\frac{2��}{3}$�Գƣ�
������ȷ���������Ǣ٢ڢۢܣ�������Ϊ��ȷ�������Ŷ����ϣ���
���� ���������ø����ǹ�ʽ�����Һ�����ͼ������ʣ��ó����ۣ�
��� �⣺�ߺ���$f��x��=cos2x+\sqrt{3}sin2x$=2��$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x��=2cos��2x-$\frac{��}{3}$����
�ʢ���ȷ��
�ߵ�$x=k��+\frac{��}{6}$��k��Z��ʱ������f��x��ȡ�����ֵΪ2���ʢ���ȷ��
��x1��x2����f��x1��=f��x2��=0����x1��x2Ϊ����f��x������㣬x1��x2��������ڵ���������
��${x_1}-{x_2}=\frac{k��}{2}��k��Z��k��0��$���ʢ���ȷ��
��x=$\frac{2��}{3}$ʱ��f��x��=2cos��=-2��Ϊ��������Сֵ���ʺ���f��x����ͼ�����ֱ��$x=\frac{2��}{3}$�Գƣ�
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢܣ�
���� ������Ҫ���鸨���ǹ�ʽ�����Һ�����ͼ������ʣ������е��⣮

��ϰ��ϵ�д�
�����Ŀ
2����֪�Ǧ����ձ߾����㣨-6��8������cos��=��������
| A�� | $\frac{4}{5}$ | B�� | $\frac{3}{5}$ | C�� | $-\frac{3}{5}$ | D�� | $-\frac{4}{5}$ |
20����֪����y=$\frac{sinx}{x}$+$\sqrt{x}$+2����y��=$\frac{xcosx-sinx}{{x}^{2}}+\frac{1}{2\sqrt{x}}$��
17��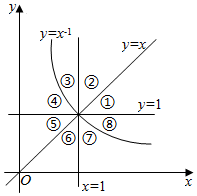 ��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������
��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������
 ��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������
��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������| A�� | y=x2 | B�� | $y=\frac{1}{{\sqrt{x}}}$ | C�� | $y={x^{\frac{1}{2}}}$ | D�� | y=x-2 |