题目内容
8.已知平面向量$\overrightarrow{a}$=(2,1),$\overrightarrow{c}$=(1,-1),若向量$\overrightarrow{b}$满足($\overrightarrow{a}$-$\overrightarrow{b}$)∥$\overrightarrow{c}$,($\overrightarrow{a}$+$\overrightarrow{c}$)⊥$\overrightarrow{b}$,则向量$\overrightarrow{b}$=( )| A. | (2,1) | B. | (1,2) | C. | (3,0) | D. | (0,3) |
分析 利用向量垂直与数量积的关系、向量共线定理即可得出.
解答 解:设$\overrightarrow{b}$=(x,y),
$\overrightarrow{a}$-$\overrightarrow{b}$=(2-x,1-y),
$\overrightarrow{a}+\overrightarrow{c}$=(3,0),
∵($\overrightarrow{a}$-$\overrightarrow{b}$)∥$\overrightarrow{c}$,($\overrightarrow{a}$+$\overrightarrow{c}$)⊥$\overrightarrow{b}$,
∴1-y+2-x=0,3x=0,
解得x=0,y=3.
则向量$\overrightarrow{b}$=(0,3),
故选:D.
点评 本题考查了向量垂直与数量积的关系、向量共线定理、向量的坐标运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.已知不等式mx2+nx-$\frac{1}{m}$<0的解集为{x|x<-$\frac{1}{2}$或x>2},则m-n=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$ | D. | -$\frac{1}{2}$ |
17.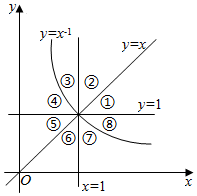 如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
 如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )| A. | y=x2 | B. | $y=\frac{1}{{\sqrt{x}}}$ | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x-2 |