题目内容
已知复数z=
，则复数z对应的点的轨迹是 ．
| 2a+(1-a2)i |
| 1+a2 |
考点：复数代数形式的混合运算,轨迹方程
专题：数系的扩充和复数
分析：利用复数的运算法则和几何意义即可得出．
解答：
解：∵复数z=
=
+
i，
令z=x+yi（x，y∈R），则
，
∴x2+y2=(
)2+(
)2=
=1，
故复数z对应的点的轨迹是x2+y2=1．
故答案为：x2+y2=1．
| 2a+(1-a2)i |
| 1+a2 |
| 2a |
| 1+a2 |
| 1-a2 |
| 1+a2 |
令z=x+yi（x，y∈R），则
|
∴x2+y2=(
| 2a |
| 1+a2 |
| 1-a2 |
| 1+a2 |
| (1+a2)2 |
| (1+a2)2 |
故复数z对应的点的轨迹是x2+y2=1．
故答案为：x2+y2=1．
点评：利用复数的运算法则和几何意义即可得出．
练习册系列答案
相关题目
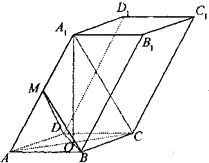已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AC∩BD=O，AA1=2