题目内容
已知A、B、C是直线l上不同的三点，O是l外一点，向量
，
，
满足：
-（
x2+1）•
-[ln（2+3x）-y]•
=
．记y=f（x）．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）若对任意x∈[
，
]不等式|a-lnx|-ln[f′（x）-3x]＞0恒成立，求实数a的取值范围：
| OA |
| OB |
| OC |
| OA |
| 3 |
| 2 |
| OB |
| OC |
| 0 |
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）若对任意x∈[
| 1 |
| 6 |
| 1 |
| 3 |
考点：函数恒成立问题,平面向量数量积的运算
专题：函数的性质及应用
分析：（Ⅰ）三点关系的等价条件，建立条件关系即可求出函数y=f（x）的解析式；
（Ⅱ）求函数的导数，将不等式|a-lnx|-ln[f′（x）-3x]＞0恒成立进行参数分离，然后求出对应函数的最小值与最大值，即可求得结论；
（Ⅱ）求函数的导数，将不等式|a-lnx|-ln[f′（x）-3x]＞0恒成立进行参数分离，然后求出对应函数的最小值与最大值，即可求得结论；
解答：
解：（Ⅰ）向量
，
，
满足：
-（
x2+1）•
-[ln（2+3x）-y]•
=
．
即
=（
x2+1）•
+[ln（2+3x）-y]•
，
∵A、B、C是直线l上不同的三点
∴（
x2+1）+[ln（2+3x）-y]=1，
即y=
x2+ln（2+3x），
∴f（x）=
x2+ln（2+3x）；
（Ⅱ）∵f（x）=
x2+ln（2+3x），
∴f'（x）=3x+
，
∴原不等式|a-lnx|-ln[f′（x）-3x]＞0等价为|a-lnx|-ln
＞0．
即|a-lnx|＞1n
．
∴a＞lnx+1n
=ln
或a＜lnx-1n
=ln
．
设h（x）=ln
，g（x）=ln
．
∵x∈[
，
]时，函数y=
，和y=
都是增函数，
∴函数h（x）=ln
，g（x）=ln
也是增函数．
∴当且进行a＜g（
）或a＞h（
），
即a＜ln
或a＞ln
．
| OA |
| OB |
| OC |
| OA |
| 3 |
| 2 |
| OB |
| OC |
| 0 |
即
| OA |
| 3 |
| 2 |
| OB |
| OC |
∵A、B、C是直线l上不同的三点
∴（
| 3 |
| 2 |
即y=
| 3 |
| 2 |
∴f（x）=
| 3 |
| 2 |
（Ⅱ）∵f（x）=
| 3 |
| 2 |
∴f'（x）=3x+
| 3 |
| 2+3x |
∴原不等式|a-lnx|-ln[f′（x）-3x]＞0等价为|a-lnx|-ln
| 3 |
| 2+3x |
即|a-lnx|＞1n
| 3 |
| 2+3x |
∴a＞lnx+1n
| 3 |
| 2+3x |
| 3x |
| 2+3x |
| 3 |
| 2+3x |
| 2x+3x2 |
| 3 |
设h（x）=ln
| 3x |
| 2+3x |
| 2x+3x2 |
| 3 |
∵x∈[
| 1 |
| 6 |
| 1 |
| 3 |
| 3x |
| 2+3x |
| 2x+3x2 |
| 3 |
∴函数h（x）=ln
| 3x |
| 2+3x |
| 2x+3x2 |
| 3 |
∴当且进行a＜g（
| 1 |
| 6 |
| 1 |
| 3 |
即a＜ln
| 5 |
| 36 |
| 1 |
| 3 |
点评：本题主要考查不等式恒成立的应用，考查向量知识，考查函数的单调性与最值，利用三点关系的等价条件，以及复合函数的单调性之间的关系是解决本题的关键，综合性较强，运算量较大．
练习册系列答案
相关题目
下列命题是真命题的是（ ）
| A、“若x=2，则（x-2）（x-1）=0” |
| B、“若x=0，则xy=0”的否命题 |
| C、“若x=0，则xy=0”的逆命题 |
| D、“若x＞1，则x＞2”的逆否命题 |
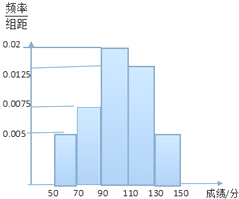某班学生参加科普知识竞赛，成绩的频率分布直方图如图，数据的分布组依次为[50，70），[70，90），[90，110），[110，130），[130，150），已知成绩低于90分的学生人数为10人．
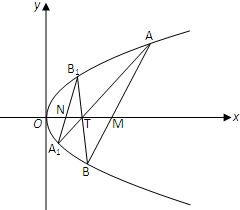已知直线l：y=2x-4与抛物线C：y2=4x相交于A，B两点，T（t，0）（t＞0且t≠2）为x轴上任意一点，连接AT，BT并延长与抛物线C分别相交于A1，B1．