题目内容
已知函数f（x）=x2+（lga-2）x+lgb满足f（1）=0，
（1）求a+b的最小值及此时a与b的值；
（2）对于任意x∈R，恒有f（x）≥2x-6成立．求a的取值范围．
（1）求a+b的最小值及此时a与b的值；
（2）对于任意x∈R，恒有f（x）≥2x-6成立．求a的取值范围．
考点：函数恒成立问题,二次函数的性质
专题：函数的性质及应用
分析：（1）根据对数的运算性质，结合基本不等式即可求a+b的最小值及此时a与b的值；
（2）根据一元二次不等式恒成立的性质将条件转化为△≤0，解不等式即可得到结论．
（2）根据一元二次不等式恒成立的性质将条件转化为△≤0，解不等式即可得到结论．
解答：
解：（1）由f（1）=lga+lgb-1=0可知：
lga+lgb=1，
即lgab=1，
∴ab=10且a，b＞0．
∴a+b≥2
=2
，当且仅当a=b=
时取等号．
即当a=b=
时，a+b有最小值2
．
（2）又f（x）≥2x-6对x∈R恒成立，
即x2+（lga-4）x+lgb+6≥0恒成立，
即x2+（lga-4）x+7-lga≥0对x∈R恒成立，
故△=（lga-4）2-4（7-lga）=lg2a-4lga-12≤0，
解得：-2≤lga≤6，
则
≤a≤106．
lga+lgb=1，
即lgab=1，
∴ab=10且a，b＞0．
∴a+b≥2
| ab |
| 10 |
| 10 |
即当a=b=
| 10 |
| 10 |
（2）又f（x）≥2x-6对x∈R恒成立，
即x2+（lga-4）x+lgb+6≥0恒成立，
即x2+（lga-4）x+7-lga≥0对x∈R恒成立，
故△=（lga-4）2-4（7-lga）=lg2a-4lga-12≤0，
解得：-2≤lga≤6，
则
| 1 |
| 100 |
点评：本题主要考查函数恒成立问题，将函数恒成立转化为一元二次函数判别式之间的关系是解决本题的关键．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
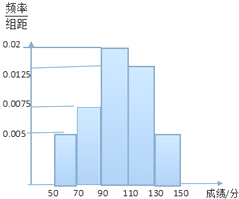某班学生参加科普知识竞赛，成绩的频率分布直方图如图，数据的分布组依次为[50，70），[70，90），[90，110），[110，130），[130，150），已知成绩低于90分的学生人数为10人．
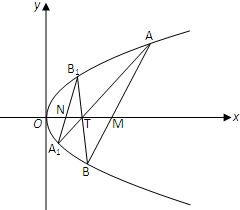已知直线l：y=2x-4与抛物线C：y2=4x相交于A，B两点，T（t，0）（t＞0且t≠2）为x轴上任意一点，连接AT，BT并延长与抛物线C分别相交于A1，B1．