题目内容
已知函数f(x)=|2x-m|和 g(x)=-x2+c(m,c为常数),且对任意x∈R,都有f(x+3)=f(-x)恒成立.
(Ⅰ)求m的值;
(Ⅱ)设函数F(x)满足对任意x∈R,都有F(x)=F(-x),且当x∈[0,3]时,F(x)=f(x).若存在x1,x2∈[-1,3],使得|F(x1)-g(x2)|<1成立,求实数c的取值范围.
(Ⅰ)求m的值;
(Ⅱ)设函数F(x)满足对任意x∈R,都有F(x)=F(-x),且当x∈[0,3]时,F(x)=f(x).若存在x1,x2∈[-1,3],使得|F(x1)-g(x2)|<1成立,求实数c的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)根据f(x+3)=f(-x),得到函数关于直线x=
对称,即可求m的值;
(Ⅱ)由条件得到函数F(x)为偶函数,然后将不等式恒成立转化为求函数的最值问题即可求出c的取值范围.
| 3 |
| 2 |
(Ⅱ)由条件得到函数F(x)为偶函数,然后将不等式恒成立转化为求函数的最值问题即可求出c的取值范围.
解答:
解:(Ⅰ)∵f(x)=|2x-m|=2|x-
|,
对任意x∈R都有;f(x+3)=f(-x),
∴f(x)关于直线x=
对称,
即
=
,解得m=3.
∴f(x)=|2x-3|
(Ⅱ)∵F(x)满足对任意x∈R,都有F(x)=F(-x),
∴F(x)是偶函数,
0≤x≤
时:F(x)=f(x)=|2x-3|=3-2x
≤x≤3时:F(x)=f(x)=|2x-3|=2x-3
∵F(x)是偶函数
∴-
≤x≤0时,0≤-x≤
,F(-x)=3+2x=F(x)
∴-1≤x≤0时:F(x)=3+2x
∴在区间[-1,3]上F(x)最大值为3,最小值为0
若存在x1和x2属于[-1,3],恒有|F(x1)-g(x2)|<1成立.
即是说明:g(x)在区间[-1,3]上的最大值或者最小值与F(x)的最大值或者最小值之间的差值在1之内,
g(x)=-x2+c在[-1,3]之间的最大值为c,最小值为x=3时取得为c-9,
∴|0-c|<1或者|3-(c-9)|<1或者|3-c|<1或者|0-(c-9)|<1
解得:-1<c<1或者11<c<13或者2<c<4或者8<c<10
∴c的取值范围为(-1,13).
| m |
| 2 |
对任意x∈R都有;f(x+3)=f(-x),
∴f(x)关于直线x=
| 3 |
| 2 |
即
| m |
| 2 |
| 3 |
| 2 |
∴f(x)=|2x-3|
(Ⅱ)∵F(x)满足对任意x∈R,都有F(x)=F(-x),
∴F(x)是偶函数,
0≤x≤
| 3 |
| 2 |
| 3 |
| 2 |
∵F(x)是偶函数
∴-
| 3 |
| 2 |
| 3 |
| 2 |
∴-1≤x≤0时:F(x)=3+2x
∴在区间[-1,3]上F(x)最大值为3,最小值为0
若存在x1和x2属于[-1,3],恒有|F(x1)-g(x2)|<1成立.
即是说明:g(x)在区间[-1,3]上的最大值或者最小值与F(x)的最大值或者最小值之间的差值在1之内,
g(x)=-x2+c在[-1,3]之间的最大值为c,最小值为x=3时取得为c-9,
∴|0-c|<1或者|3-(c-9)|<1或者|3-c|<1或者|0-(c-9)|<1
解得:-1<c<1或者11<c<13或者2<c<4或者8<c<10
∴c的取值范围为(-1,13).
点评:本题主要考查函数奇偶性和对称性的应用,将不等式恒成立转化为求函数的最值是解决本题的关键,综合性较强,运算量较大.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |
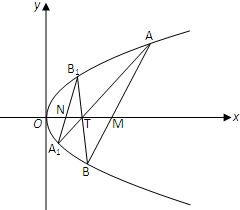 已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.
已知直线l:y=2x-4与抛物线C:y2=4x相交于A,B两点,T(t,0)(t>0且t≠2)为x轴上任意一点,连接AT,BT并延长与抛物线C分别相交于A1,B1.