题目内容
（1）将圆心角为120°，面积为3π的扇形，作为圆锥的侧面，求圆锥的表面积和体积；
（2）在△ABC中，满足：
⊥
，|
|=|
|，求向量
+2
与向量2
+
的夹角的余弦值．
（2）在△ABC中，满足：
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
考点：平面向量数量积的运算,旋转体（圆柱、圆锥、圆台）
专题：平面向量及应用,空间位置关系与距离
分析：（1）先求出圆锥的母线以及底面半径，再计算S表面积与体积V；
（2）根据题意，通过数量积求出两向量夹角的余弦值．
（2）根据题意，通过数量积求出两向量夹角的余弦值．
解答：
解：（1）设扇形的半径和圆锥的母线都为l，圆锥的半径为r，则
πl2=3π，得l=3；
×3=2πr，得r=1；
∴S表面积=S侧面+S底面=πrl+πr2=4π，
∴V=
Sh=
×π×12×2
=
π．
（2）设向量
+2
与向量2
+
的夹角为θ，则
cosθ=
，
令|
|=|
|=a，
且
⊥
，
∴
•
=0；
∴cosθ=
=
．
| 120 |
| 360 |
| 2π |
| 3 |
∴S表面积=S侧面+S底面=πrl+πr2=4π，
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
（2）设向量
| AB |
| AC |
| AB |
| AC |
cosθ=
(
| ||||||||
|
|
令|
| AB |
| AC |
且
| AB |
| AC |
∴
| AB |
| AC |
∴cosθ=
| 2a2+2a2 | ||||
|
| 4 |
| 5 |
点评：本题考查了锥体的表面积与体积的计算问题以及平面向量的夹角问题，是基础题．
练习册系列答案
优学名师名题系列答案
相关题目
若（2x+1）n=a0+a1x+…+aixi+…+anxn，其中n∈N*，则a1-22a2+…+（-1）n+1n2an=（ ）
| A、（-1）n+1•2•（5n-4） |
| B、（-1）n+1•6•（3n-2） |
| C、2n（2n+1）•3n-2 |
| D、（-1）n+1•2n（2n-1） |
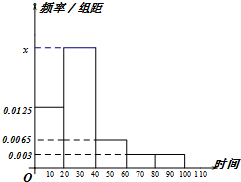某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
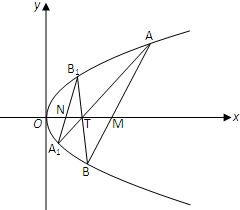已知直线l：y=2x-4与抛物线C：y2=4x相交于A，B两点，T（t，0）（t＞0且t≠2）为x轴上任意一点，连接AT，BT并延长与抛物线C分别相交于A1，B1．