题目内容
16.已知菱形ABCD如图(1)所示,其中∠ACD=60°,AB=2,AC与BD相交于点O,现沿AC进行翻折,使得平面ACD⊥平面ABC,取点E,连接AE,BE,CE,DE,使得线段BE再平面ABC内的投影落在线段OB上,得到的图形如图(2)所示,其中∠OBE=60°,BE=2.(Ⅰ)证明:DE⊥AC;
(Ⅱ)求二面角A-BE-C的余弦值.
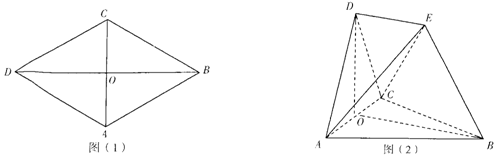
分析 (Ⅰ)依题意得DO⊥AC.,又平面ACD⊥平面ABC,得DO⊥面ABC.
作EF⊥面ABC于F,可得F落在BO上,可得四边形DEFO是矩形,即证得 DE⊥AC
(Ⅱ)以O为原点,OA,OB,OD所在直线分别为x、y、z轴建立空间直角坐标系,
则A(1,0,0),B(0,$\sqrt{3}$,0),C(-1,0,0),E(0,$\sqrt{3}-1,\sqrt{3}$).利用向量求解.
解答 解:(Ⅰ)证明:依题意得△ABC,△ACD都是边长为2的等边三角形,∴DO⊥AC.
又平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,DO?面ACD,∴DO⊥面ABC.
作EF⊥面ABC于F,可得F落在BO上,且∠EBF=∠OBE=60°.
在Rt△BEF中,EF=BE$•sin∠EBF=\sqrt{3}$,
在Rt△DOC中,DO=DC$•sin∠DCO=\sqrt{3}$,
∵DO⊥面ABC,EF⊥面ABC,所以DO∥EF,又DO=EF,∴四边形DEFO是矩形,
∵OF⊥AC,∴DE⊥AC;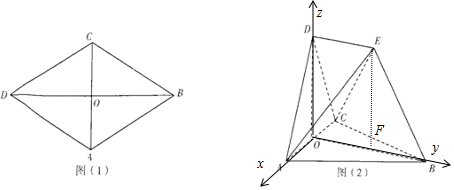
(Ⅱ)以O为原点,OA,OB,OD所在直线分别为x、y、z轴建立空间直角坐标系,
则A(1,0,0),B(0,$\sqrt{3}$,0),C(-1,0,0),E(0,$\sqrt{3}-1,\sqrt{3}$).
故$\overrightarrow{BE}=(0,-1,\sqrt{3}$),$\overrightarrow{BC}=(-1,-\sqrt{3},0)$.
设平面BCE的法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BE}=-y+\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{BC}=-x-\sqrt{3}y=0}\end{array}\right.$,可取$\overrightarrow{n}=(-3,\sqrt{3},1)$
设平面ABE的法向量为$\overrightarrow{m}=(a,b,c)$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{EB}=-b+\sqrt{3}c=0}\\{\overrightarrow{m}•\overrightarrow{AB}=-a+\sqrt{3}b=0}\end{array}\right.$,可取$\overrightarrow{m}=(3,\sqrt{3},1)$
cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=-$\frac{5}{13}$,
∴二面角A-BE-C的余弦值为$\frac{5}{13}$.
点评 本题考查了空间面面垂直的性质,线线垂直的判定,向量法求二面角,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {x|x>-2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|-2<x<2} |
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)的图象关于y轴对称,则下列结论中正确的是( )
| A. | f(4.5)<f(7)<f(6.5) | B. | f(7)<f(4.5)<f(6.5) | C. | f(7)<f(6.5)<f(4.5) | D. | f(4.5)<f(6.5)<f(7) |
| A. | 存在R上函数g(x),使得f(g(x))=x | B. | 存在R上函数g(x),使得g(f(x))=x | ||
| C. | 存在R上函数g(x),使得f(g(x))=g(x) | D. | 存在R上函数g(x),使得f(g(x))=g(f(x)) |