��Ŀ����
4����ƽ��ֱ������ϵxOy�У���֪����C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ����������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ��=sin�ȣ�����������C1�ļ����귽�̼�����C2��ֱ�����귽�̣�
������֪����C1��C2����O��A���㣬��O���Ҵ�ֱ��OA��ֱ��������C1��C2����M��N���㣬��|MN|��ֵ��
���� ��I������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ������������ƽ����ϵ�ɵ���ͨ���̣����û�����ʽ�ɵã�����C1�ļ����귽�̣�����C2�ļ����귽��Ϊ��=sin�ȣ��ɵã���2=��sin�ȣ����û�����ʽ�ɵã�����C2��ֱ�����귽�̣�
��II������$\left\{\begin{array}{l}{��=2cos��}\\{��=sin��}\end{array}\right.$���ɵ�tan��=2�����A�ļ���Ϊ�ȣ���tan��=2���ɵ�sin��=$\frac{2\sqrt{5}}{5}$��cos��=$\frac{\sqrt{5}}{5}$����M$��{��}_{1}����-\frac{��}{2}��$�������=2cos�ȣ��ɵã���1��N$��{��}_{2}����+\frac{��}{2}��$�������=sin�ȣ��ɵã���2���ɵã�|MN|=��1+��2��
��� �⣺��I������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
����ƽ����ϵ�ɵã���x-1��2+y2=1����Ϊx2+y2-2x=0��
���û�����ʽ�ɵã�����C1�ļ����귽��Ϊ��2-2��cos��=0������=2cos�ȣ�
����C2�ļ����귽��Ϊ��=sin�ȣ��ɵã���2=��sin�ȣ��ɵã�����C2��ֱ�����귽��Ϊx2+y2=y��
��II������$\left\{\begin{array}{l}{��=2cos��}\\{��=sin��}\end{array}\right.$���ɵ�tan��=2�����A�ļ���Ϊ�ȣ���tan��=2���ɵ�sin��=$\frac{2\sqrt{5}}{5}$��cos��=$\frac{\sqrt{5}}{5}$��
��M$��{��}_{1}����-\frac{��}{2}��$�������=2cos�ȣ��ɵã���1=2cos$����-\frac{��}{2}��$=2sin��=$\frac{4\sqrt{5}}{5}$��
N$��{��}_{2}����+\frac{��}{2}��$�������=sin�ȣ��ɵã���2=sin$����+\frac{��}{2}��$=cos��=$\frac{\sqrt{5}}{5}$��
�ɵã�|MN|=��1+��2=$\sqrt{5}$��
���� ���⿼���˲������̻�Ϊ��ͨ���̡������귽����ֱ�����귽�̵Ļ�����Բ�ཻ�ҳ����⣬������������������������������е��⣮

| A�� | 4 | B�� | -6 | C�� | -10 | D�� | 10 |
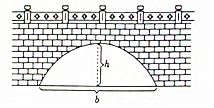 һ���ŵ���״Ϊ�����ߣ��������߹��ĸ�Ϊh����Ϊb���������߹������ΪS����b=3h����S���ڣ�������
һ���ŵ���״Ϊ�����ߣ��������߹��ĸ�Ϊh����Ϊb���������߹������ΪS����b=3h����S���ڣ�������| A�� | h2 | B�� | $\frac{3}{2}$h2 | C�� | $\sqrt{3}$h2 | D�� | 2h2 |