题目内容
7．已知定义在R上的函数y=f（x）满足以下三个条件：①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称，则下列结论中正确的是（ ）
| A． | f（4.5）＜f（7）＜f（6.5） | B． | f（7）＜f（4.5）＜f（6.5） | C． | f（7）＜f（6.5）＜f（4.5） | D． | f（4.5）＜f（6.5）＜f（7） |
分析 利用已知条件判断函数的性质，然后推出结果即可．
解答 解：定义在R上的函数y=f（x）满足以下三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称，
可知函数是周期为4的函数，x∈[0，2]函数是增函数，函数的对称轴为x=2，
f（4.5）=f（0.5），f（7）=f（3）=f（1），f（6.5）=f（2.5）=f（1.5），
可得f（4.5）＜f（7）＜f（6.5）．
故选：A．
点评 本题考查函数与方程的综合应用，函数的对称轴周期性以及单调性的应用，考查计算能力．
练习册系列答案
相关题目
17．记不等式组$\left\{\begin{array}{l}4x+3y≥10\\ x≤3\\ y≤4\end{array}\right.$表示的平面区域为D，过区域D中任意一点P作圆x2+y2=1的两条切线，切点分别为A，B，则cos∠PAB的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
18．若函数f（x）=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+x（a∈R+）在区间[2，4]上为单调递增函数，则$\frac{25}{a}$+a的取值范围为（ ）
| A． | [10，+∞） | B． | [$\frac{29}{2}$，+∞） | C． | [$\frac{25}{2}$，+∞） | D． | [$\frac{41}{4}$，+∞） |
12．
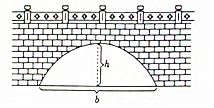一拱桥的形状为抛物线，该抛物线拱的高为h，宽为b，此抛物线拱的面积为S，若b=3h，则S等于（ ）
一拱桥的形状为抛物线，该抛物线拱的高为h，宽为b，此抛物线拱的面积为S，若b=3h，则S等于（ ）| A． | h2 | B． | $\frac{3}{2}$h2 | C． | $\sqrt{3}$h2 | D． | 2h2 |
