题目内容
1.定义max{a,b}=$\left\{\begin{array}{l}{a,a≥b}\\{b,a<b}\end{array}\right.$,已知函数f(x)=max{|2x-1|,ax2+b},其中a<0,b∈R,若f(0)=b,则实数b的范围为[1,+∞),若f(x)的最小值为1,则a+b=1.分析 利用定义判断b的范围,作出两函数y=|2x-1|与y=ax2+b的函数图象,根据f(x)定义判断y=ax2+b与点(1,1)的关系,得出a+b的值.
解答 解:∵f(0)=max{1,b}=b,∴b≥1;
作出y=|2x-1|与y=ax2+b的函数图象,如图所示:
∵f(x)的最小值为1,∴y=ax2+b恰好经过点(1,1),
∴a+b=1.
故答案为:[1,+∞),1.
点评 本题考查了函数图象的关系,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
11.要得到函数y=sin(5x-$\frac{π}{4}$)的图象,只需将函数y=cos5x的图象( )
| A. | 向左平移$\frac{3π}{20}$个单位 | B. | 向右平移$\frac{3π}{20}$个单位 | ||
| C. | 向左平移$\frac{3π}{4}$个单位 | D. | 向右平移$\frac{3π}{4}$个单位 |
12.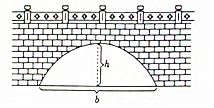 一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )
一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )
 一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )
一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )| A. | h2 | B. | $\frac{3}{2}$h2 | C. | $\sqrt{3}$h2 | D. | 2h2 |