题目内容
8.已知角α终边上一点P(-4,3),求$\frac{{sin(α-2π)+cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(π-α)+cos(\frac{11π}{2}-α)sin(\frac{3π}{2}+α)}}$.分析 先根据角α终边上一点P确定tanα的值,进而利用诱导公式对原式进行化简整理后,把tanα的值代入即可.
解答 解:∵角α终边上一点P(-4,3),
∴tanα=$\frac{y}{x}$=-$\frac{3}{4}$,
∴$\frac{{sin(α-2π)+cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(π-α)+cos(\frac{11π}{2}-α)sin(\frac{3π}{2}+α)}}$=$\frac{sinα-si{n}^{2}α}{-cosα(1-sinα)}$=-tanα=$\frac{3}{4}$.
点评 本题主要考查了运用诱导公式化简求值的问题.要特别留意在三角函数转换过程中三角函数的正负号的判定,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.若f(x)=(a-3)x${\;}^{{a}^{2}-3a-2}$既是幂函数又是二次函数,则a的值是( )
| A. | -1 | B. | 4 | C. | -1或4 | D. | 2 |
13.已知函数f(x)=$\left\{\begin{array}{l}{e^x+a,x≤0}\\{3x-1,x>0}\end{array}\right.$(a∈R),若函数f(x)在R上有两个零点,则a的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,0) | C. | (-1,0) | D. | [-1,0) |
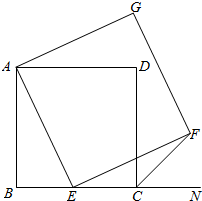 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.