若fx${\;}^{{a}^{2}-3a-2}$既是幂函数又是二次函数.则a的值是( )A．-1B．4C．-1或4D．2 题目和参考答案——青夏教育精英家教网—

题目内容

11．若f（x）=（a-3）x${\;}^{{a}^{2}-3a-2}$既是幂函数又是二次函数，则a的值是（　　）

A．

-1

B．

C．

-1或4

D．

分析利用幂函数的定义求出a值，判断函数是二次函数即可得到结果．

解答解：f（x）=（a-3）x${\;}^{{a}^{2}-3a-2}$是幂函数．可得a-3=1，解得a=4，
当a=4时，a²-3a-2=2，满足函数是二次函数．
故选：B．

点评本题考查函数的解析式的求法，二次函数的性质以及幂函数的解析式的应用，考查计算能力．

练习册系列答案

学而优中考专题分类集训南京大学出版社系列答案

2．函数y=$\frac{2}{\sqrt{x-4}}$的值域是（　　）

19．设f（x）的一个原函数为$\frac{1}{x}$，则f′（x）=$-\frac{1}{{x}^{2}}$．

6．已知alog₉4=1，3^b=2，则ab=1．

1．已知圆C的圆心与点P（0，1）关于直线y=x+1对称，直线3x+4y+1=0与圆C相交于A，B两点，且|AB|=4．
（1）求圆C的标准方程；
（2）设直线l：mx-y+1-m=0（m∈R）与圆C的交点为E、F，求弦EF的中点M的轨迹方程．

8．已知角α终边上一点P（-4，3），求$\frac{{sin（α-2π）+cos（\frac{π}{2}+α）sin（-π-α）}}{{cos（π-α）+cos（\frac{11π}{2}-α）sin（\frac{3π}{2}+α）}}$．

5．下列函数中是偶函数，且又在区间（-∞，0）上是增函数的是（　　）

$y={（\frac{1}{4}）^{-|x|}}$

D．

$y={log_3}{x^{\frac{5}{6}}}$

6．

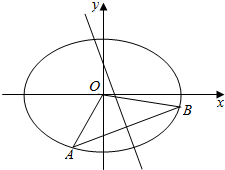已知椭圆$\frac{{x}^{2}}{2}$+y²=1上两个不同的点A，B关于直线$y=mx+\frac{1}{2}（m≠0）$对称．
（1）若已知$C（0，\frac{1}{2}）$，M为椭圆上动点，证明：$|{MC}|≤\frac{{\sqrt{10}}}{2}$；
（2）求实数m的取值范围；
（3）求△AOB面积的最大值（O为坐标原点）．

试题分类