题目内容
若变量x，y满足约束条件
，则z=5y-x的最大值是（ ）
|
| A、16 | B、30 | C、24 | D、8 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．
解答：
解：作出不等式
对应的平面区域（阴影部分），
由z=5y-x，得y=
x+
，
平移直线y=
x+
，由图象可知当直线y=
x+
经过点B时，直线y=-2x+z的截距最大，此时z最大．
由
，解得
，
即B（4，4）．
此时z的最大值为a=z=5×4-4=20-4=16，
故选：A．
解：作出不等式
|
由z=5y-x，得y=
| 1 |
| 5 |
| z |
| 5 |
平移直线y=
| 1 |
| 5 |
| z |
| 5 |
| 1 |
| 5 |
| z |
| 5 |
由
|
|
即B（4，4）．
此时z的最大值为a=z=5×4-4=20-4=16，
故选：A．
点评：本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．
练习册系列答案
相关题目
已知随机变量X服从正态分布N（3，σ2），且P（X＜2）=0.3，则P（2＜X＜4）的值等于（ ）
| A、0.5 | B、0.2 |
| C、0.3 | D、0.4 |
设?的分布列为
又设y=2?+5 则 Ey=（ ）
| ? | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=ax3+bx2+cx+d的图象如图所示，则一定有（ ）
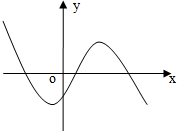
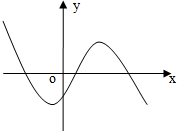
| A、a＜0 b＞0 c＞0 d＜0 |
| B、a＜0 b＜0 c＞0 d＜0 |
| C、a＜0 b＞0 c＜0 d＜0 |
| D、a＜0 b＜0 c＜0 d＜0 |
已知x1，x2∈[-
，
]，且x1sinx1-x2sinx2＜0，则下列结论正确的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、x13＜x23 |
| B、x1+x2＜0 |
| C、|x1|＞|x2| |
| D、|x1|＜|x2| |
已知a＜b＜0，则下列不等式关系中不能成立的是（ ）
A、
| ||||
B、
| ||||
| C、|a|＞|b| | ||||
| D、a4＞b4 |
设正项等比数列{an}的前n项和为Sn，且210S30+S10=（210+1）S20，则数列{an}的公比为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
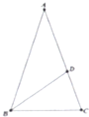学习“三角”时，小明同学在参考书上看到求sin18°精确值的一种方法，具体如下：设等腰△ABC的顶角∠A=36°．底角∠B的平分线交腰AC于D，且BC=1（如图），则AD=BD=1，于是，在△BCD中，可得CD=2sin18°．由△BAC∽△CBD得| AC |
| BC |
| BD |
| CD |
| 1+2sin18° |
| 1 |
| 1 |
| 2sin18° |
| ||
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| A、关于x的方程α•4x+β•2x+α=0有实数解 | ||
| B、关于x的方程α•（log4x）2+β•log4x-α=0无实数解 | ||
C、关于x的方程sinx=
| ||
D、关于x的方程cosx=
|