题目内容
若函数f(x)=ax3+bx2+cx+d的图象如图所示,则一定有( )
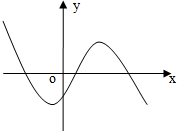
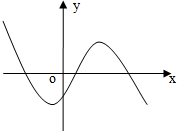
| A、a<0 b>0 c>0 d<0 |
| B、a<0 b<0 c>0 d<0 |
| C、a<0 b>0 c<0 d<0 |
| D、a<0 b<0 c<0 d<0 |
考点:函数的图象
专题:函数的性质及应用,导数的概念及应用
分析:由已知中函数f(x)=ax3+bx2+cx+d的图象,根据其与y轴交点的位置,可以判断d的符号,进而根据其单调性和极值点的位置,可以判断出其中导函数图象的开口方向(可判断a的符号)及对应函数两个根的情况,结合韦达定理,可分析出b,c的符号,进而得到答案.
解答:
解:∵函数f(x)=ax3+bx2+cx+d的图象与y轴交点的纵坐标为负,故d<0;
∵f(x)=ax3+bx2+cx+d的图象有两个递减区间,有两个递增区间,
∴f′(x)=3ax2+2bx+c的图象开口方向朝下,且于x轴有两个交点,故a<0,
又∵f(x)=ax3+bx2+cx+d的图象的极小值点和极大值点在y轴两侧,且极小点离y轴近,
∴f′(x)=3ax2+2bx+c=0的两根x1,x2满足,
x1+x2>0,则b>0,x1•x2<0,则c>0,
综上a<0,b>0,c>0,d<0,
故选A
∵f(x)=ax3+bx2+cx+d的图象有两个递减区间,有两个递增区间,
∴f′(x)=3ax2+2bx+c的图象开口方向朝下,且于x轴有两个交点,故a<0,
又∵f(x)=ax3+bx2+cx+d的图象的极小值点和极大值点在y轴两侧,且极小点离y轴近,
∴f′(x)=3ax2+2bx+c=0的两根x1,x2满足,
x1+x2>0,则b>0,x1•x2<0,则c>0,
综上a<0,b>0,c>0,d<0,
故选A
点评:本题考查的知识点是函数的图象与图象变化,其中根据图象的形状分析其导函数的性质是解答本题的关键,同时由于本题涉及到导数,二次函数的图象和性质,函数的单调性,函数取极值的条件等诸多难点,故难度比较大.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
甲、乙两人一起去游海口车展,他们约定各自独立的从1到6号展台中,任选4个进行观看,每个展台参观10分钟,则最后10分钟他们同在一个展台的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
椭圆
+
=1的焦点坐标为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、(±1,0) | ||
B、(±
| ||
| C、(±2,0) | ||
| D、(0,±1) |
运行以下程序:

得到的结果是( )

得到的结果是( )
| A、j-1 | B、j | C、10 | D、9 |
已知数列{an}中,a1=1,an+1=2an-3,则数列{an}的通项公式为( )
A、an=
| |||||
| B、an=3+(-2)n | |||||
| C、an=3-2n | |||||
| D、an=-3+2n+1 |
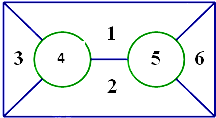 有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )| A、4320 | B、2880 |
| C、1440 | D、720 |
若变量x,y满足约束条件
,则z=5y-x的最大值是( )
|
| A、16 | B、30 | C、24 | D、8 |
方程lgx+x=0根的个数为( )
| A、无穷多 | B、3 | C、1 | D、0 |
某人从甲地到乙地有A,B,C三条路可走,走A路的概率为0.2,不走C路的概率为0.8,则该人走B路的概率是( )
| A、0.6 | B、0.3 |
| C、0.1 | D、0.5 |