题目内容
已知a<b<0,则下列不等式关系中不能成立的是( )
A、
| ||||
B、
| ||||
| C、|a|>|b| | ||||
| D、a4>b4 |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:A.由a<b<0,可得
<
,化为
<
,即可判断出;
B.由a<b<0,可得a-b<0,a(a-b)>0,作差可得
-
=
=
<0,即
<
,即可判断出;
C.由a<b<0,可得-a>-b>0,即|a|>|b|,即可判断出;
D.由C可知:|a|>|b|,进而点到a4>b4.
| a |
| ab |
| b |
| ab |
| 1 |
| b |
| 1 |
| a |
B.由a<b<0,可得a-b<0,a(a-b)>0,作差可得
| 1 |
| a-b |
| 1 |
| a |
| a-(a-b) |
| a(a-b) |
| b |
| a(a-b) |
| 1 |
| a-b |
| 1 |
| a |
C.由a<b<0,可得-a>-b>0,即|a|>|b|,即可判断出;
D.由C可知:|a|>|b|,进而点到a4>b4.
解答:
解:A.∵a<b<0,∴
<
,化为
<
,因此正确;
B.∵a<b<0,∴a-b<0,∴a(a-b)>0,∴
-
=
=
<0,∴
<
,因此B不成立;
C.∵a<b<0,∴-a>-b>0,即|a|>|b|,因此正确;
D.由C可知:|a|>|b|,∴a4>b4.
综上可知:只有B不成立.
故选:B.
| a |
| ab |
| b |
| ab |
| 1 |
| b |
| 1 |
| a |
B.∵a<b<0,∴a-b<0,∴a(a-b)>0,∴
| 1 |
| a-b |
| 1 |
| a |
| a-(a-b) |
| a(a-b) |
| b |
| a(a-b) |
| 1 |
| a-b |
| 1 |
| a |
C.∵a<b<0,∴-a>-b>0,即|a|>|b|,因此正确;
D.由C可知:|a|>|b|,∴a4>b4.
综上可知:只有B不成立.
故选:B.
点评:本题考查了不等式的基本性质、“作差法”,属于基础题.

练习册系列答案
相关题目
已知x,y为实数,若3x+5y>3-y+5-x,则( )
| A、x+y>0 |
| B、x+y<0 |
| C、x-y<0 |
| D、x-y>0 |
运行以下程序:

得到的结果是( )

得到的结果是( )
| A、j-1 | B、j | C、10 | D、9 |
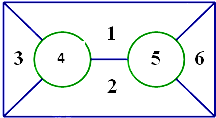 有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )| A、4320 | B、2880 |
| C、1440 | D、720 |
若变量x,y满足约束条件
,则z=5y-x的最大值是( )
|
| A、16 | B、30 | C、24 | D、8 |
已知函数f(x)的导函数为f′(x),且满足f(x)=3f′(1)•x-x4,则f′(1)=( )
| A、-1 | B、-2 | C、1 | D、2 |
方程lgx+x=0根的个数为( )
| A、无穷多 | B、3 | C、1 | D、0 |
如果执行下面的算法语句后输出结果是8,则输入的值是( )


| A、3 | B、5或12- |
| C、12 | D、4或12 |