题目内容
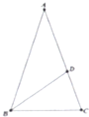 学习“三角”时,小明同学在参考书上看到求sin18°精确值的一种方法,具体如下:设等腰△ABC的顶角∠A=36°.底角∠B的平分线交腰AC于D,且BC=1(如图),则AD=BD=1,于是,在△BCD中,可得CD=2sin18°.由△BAC∽△CBD得
学习“三角”时,小明同学在参考书上看到求sin18°精确值的一种方法,具体如下:设等腰△ABC的顶角∠A=36°.底角∠B的平分线交腰AC于D,且BC=1(如图),则AD=BD=1,于是,在△BCD中,可得CD=2sin18°.由△BAC∽△CBD得| AC |
| BC |
| BD |
| CD |
| 1+2sin18° |
| 1 |
| 1 |
| 2sin18° |
| ||
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| A、关于x的方程α•4x+β•2x+α=0有实数解 | ||
| B、关于x的方程α•(log4x)2+β•log4x-α=0无实数解 | ||
C、关于x的方程sinx=
| ||
D、关于x的方程cosx=
|
考点:命题的真假判断与应用
专题:创新题型
分析:题干信息较多的选择题,应该从选项入手.
解答:
解:1 4x=(2x)2,则可以把A选项看成是一个关于2x的二元一次函数,由已知条件可知,α、β均大于0,2x也大于0,所以A选项中的所有项都是大于0的,所以其和不可能为0,故无解.
2 对于B选项可从判别式入手,得△=β2+4αβ,根据题意,α、β均大于0,所以判别式也大于0,故方程有解,B错
3 只要讨论
的绝对值小于等于1即可,即|
|≤1有解,解之,有0≤β≤α,这个解题干信息可以满足,故C有解,C正确
4 同理,只需判断|
|>1是不是恒成立,我们解不等式有:α+β<0或者α<0,显然与题干信息不符,故D错误,
故选:C
2 对于B选项可从判别式入手,得△=β2+4αβ,根据题意,α、β均大于0,所以判别式也大于0,故方程有解,B错
3 只要讨论
| 2β-α |
| α |
| 2β-α |
| α |
4 同理,只需判断|
| β |
| 2α+β |
故选:C
点评:这种题,题干信息比较多,也比较难,但选项简单易判,故应该从选项着手会更容易些.

练习册系列答案
相关题目
椭圆
+
=1的焦点坐标为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、(±1,0) | ||
B、(±
| ||
| C、(±2,0) | ||
| D、(0,±1) |
若变量x,y满足约束条件
,则z=5y-x的最大值是( )
|
| A、16 | B、30 | C、24 | D、8 |
方程lgx+x=0根的个数为( )
| A、无穷多 | B、3 | C、1 | D、0 |
设双曲线
-
=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,与双曲线的其中一个交点为P,若
=2
,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| PB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果执行下面的算法语句后输出结果是8,则输入的值是( )


| A、3 | B、5或12- |
| C、12 | D、4或12 |
三名射手独立地进行射击,甲中靶的概率是0.9,乙、丙中靶的概率均为0.8,三人中恰有两人中靶的概率( )
| A、0.352 | B、0368 |
| C、0.412 | D、0.214 |
某人从甲地到乙地有A,B,C三条路可走,走A路的概率为0.2,不走C路的概率为0.8,则该人走B路的概率是( )
| A、0.6 | B、0.3 |
| C、0.1 | D、0.5 |