题目内容
11.在△ABC中,a,b,c分别是角A,B,C的对边,b=$\sqrt{2}$sinB,且满足tanA+tanC=$\frac{2sinB}{cosA}$.(Ⅰ)求角C和边c的大小;
(Ⅱ)求△ABC面积的最大值.
分析 (Ⅰ)根据同角的三角函数的关系以及诱导公式和两角和的正弦公式即可求出,再根据正弦定理即可求出c的值,
(Ⅱ)根据余弦定理和基本不等式即可求出最大值.
解答 解:(Ⅰ)tanA+tanC=$\frac{2sinB}{cosA}$可得$\frac{sinA}{cosA}$+$\frac{sinC}{cosC}$=$\frac{sinAcosC+cosAsinC}{cosAcosC}$
=$\frac{sin(A+C)}{cosAcosC}$=$\frac{sinB}{cosAcosC}$=$\frac{2sinB}{cosA}$,
∴cosC=$\frac{1}{2}$,
∵0<C<π,
∴C=$\frac{π}{3}$,
∵b=$\sqrt{2}$sinB,
由正弦定理可得$\frac{c}{sinC}$=$\frac{b}{sinB}$=$\sqrt{2}$,
∴c=$\frac{\sqrt{6}}{2}$;
(Ⅱ)由余弦定理可得c2=a2+b2-2abcosC,
∴$\frac{3}{2}$=a2+b2-ab≥2ab-ab=ab,当且仅当a=b时取等号.
∴S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}$×$\frac{3}{2}$=$\frac{3\sqrt{3}}{8}$,
故△ABC面积的最大值为$\frac{3\sqrt{3}}{8}$..
点评 本题考查了正弦定理和余弦定理以及三角函数的恒等变换,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体中最长的棱长为( )
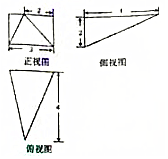

| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
16.某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
表2
已知表1数据的中位数估计值为26,回答以下问题.
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
表1
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
3.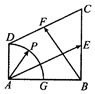 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
20.已知函数f'(x)是函数f(x)的导函数,$f(1)=\frac{1}{e}$,对任意实数都有f(x)-f'(x)>0,则不等式f(x)<ex-2的解集为( )
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |