题目内容
17.$\overrightarrow{ab}$表示一个两位数,十位数和个位数分别用a,b表示,记f($\overrightarrow{ab}$)=a+b+3ab,如f($\overrightarrow{12}$)=1+2+3×1×2=9,则满足f($\overrightarrow{ab}$)=$\overrightarrow{ab}$的两位数的个数为( )| A. | 15 | B. | 13 | C. | 9 | D. | 7 |
分析 由题意,a+b+3ab=10a+b,求出b的值,再判断a即可得到答案
解答 解:由题意,a+b+3ab=10a+b,解得b=3,
a取1到9,共9个,
故选:C
点评 本题考查了简单的计数原理,属于基础题.

练习册系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体中最长的棱长为( )
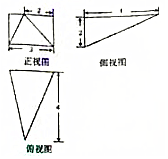

| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
20.已知函数f'(x)是函数f(x)的导函数,$f(1)=\frac{1}{e}$,对任意实数都有f(x)-f'(x)>0,则不等式f(x)<ex-2的解集为( )
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
6.函数f(x)=$\frac{6x}{{1+{x^2}}}$在区间[0,3]的最大值为( )
| A. | 3 | B. | 4 | C. | 2 | D. | 5 |
7.已知α是锐角,若cos(α+$\frac{π}{6}$)=$\frac{5}{13}$,则sin(α-$\frac{π}{12}$)=( )
| A. | -$\frac{17\sqrt{2}}{26}$ | B. | -$\frac{7\sqrt{2}}{26}$ | C. | $\frac{7\sqrt{2}}{26}$ | D. | $\frac{17\sqrt{2}}{26}$ |
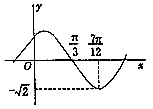 (1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域; 如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°
如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°