题目内容
15．直线y=kx+3（k≠0）与圆（x-3）2+（y-2）2=4相交于A、B两点，若$|AB|=2\sqrt{3}$，则k的值为$-\frac{3}{4}$．分析 由弦长公式得，当圆心到直线的距离等于1时，弦长$|AB|=2\sqrt{3}$，解此方程求出k的取值即可．
解答 解：圆（x-3）2+（y-2）2=4圆心坐标（3，2），半径为2，
因为直线y=kx+3与圆（x-3）2+（y-2）2=4相交于A、B两点，$|AB|=2\sqrt{3}$，
由弦长公式得，圆心到直线的距离等于1，
即$\frac{|3k-2+3|}{\sqrt{1+{k}^{2}}}$=1，8k（k+$\frac{3}{4}$）=0，
得：k=-$\frac{3}{4}$，
故答案为：$-\frac{3}{4}$．
点评 本题考查圆心到直线的距离公式的应用，以及弦长公式的应用．考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}），{F_1}$为左焦点，A为右顶点，B1，B2分别为上、下顶点，若F1，A，B1，B2四点在同一圆上，则此椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{3}-1}}{2}$ | B． | $\frac{{\sqrt{5}-1}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
10．如图的三视图所对应的立体图形可以是（ ）
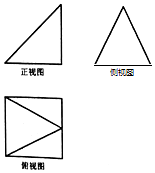
| A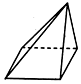． |  | B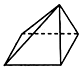． |  | C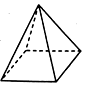． |  | D． |  |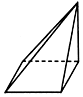
7．已知圆C：x2+y2=4上所有的点满足约束条件$\left\{\begin{array}{l}{x+y+4≥0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$，当m取最小值时，可行域（不等式组所围成的平面区域）的面积为（ ）
| A． | 48 | B． | 54 | C． | 24$\sqrt{2}$ | D． | 36$\sqrt{3}$ |
16．200件产品有5件次品，先从中任意抽去5间，其中至少有2件次品的抽法有（ ）
| A． | A${\;}_{3}^{2}$C${\;}_{197}^{3}$+C${\;}_{3}^{3}$C${\;}_{197}^{2}$种 | |
| B． | C${\;}_{3}^{2}$C${\;}_{198}^{3}$种 | |
| C． | C${\;}_{200}^{5}$-C${\;}_{197}^{5}$种 | |
| D． | C${\;}_{200}^{5}$-C${\;}_{3}^{1}$C${\;}_{197}^{4}$种 |