题目内容
6.已知双曲线与椭圆$\frac{x^2}{16}+\frac{y^2}{3}=1$有相同的焦点,且其中一条渐近线为$y=\frac{3}{2}x$,则该双曲线的标准方程是$\frac{x^2}{4}-\frac{y^2}{9}=1$.分析 求出椭圆的焦点坐标,得到双曲线的焦点坐标,利用双曲线的渐近线方程,求出a,b,即可得到双曲线方程.
解答 解:双曲线与椭圆$\frac{x^2}{16}+\frac{y^2}{3}=1$有相同的焦点($±\sqrt{13}$,0),焦点坐标在x轴,双曲线的一条渐近线为$y=\frac{3}{2}x$,
可得$\frac{b}{a}$=$\frac{3}{2}$,a2+b2=13,可得a2=4,b2=9.
所求双曲线方程为:$\frac{x^2}{4}-\frac{y^2}{9}=1$.
故答案为:$\frac{x^2}{4}-\frac{y^2}{9}=1$.
点评 本题考查椭圆的简单性质以及双曲线的简单性质的应用,双曲线方程的求法,考查计算能力.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
1.已知空间两点A(3,3,1),B(-1,1,5),则线段AB的长度为( )
| A. | 6 | B. | $2\sqrt{6}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{14}$ |
11.已知函数$f(x)=\sqrt{x}sinx$,则f'(π)=( )
| A. | $\sqrt{π}$ | B. | $-\sqrt{π}$ | C. | $\frac{{\sqrt{π}}}{2π}$ | D. | $\frac{{\sqrt{2π}}}{2π}$ |
18.阅读如图的程序框图,运行相应的程序,则输出的T的值为( )


| A. | 57 | B. | 120 | C. | 183 | D. | 247 |
8.从集合{a,b,c,d,e}的所有子集中,任取一个,所取集合恰是集合{a,b,c}子集的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
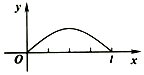
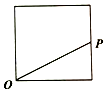 点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )
点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )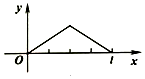


 如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.
如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.