题目内容
设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}是等差数列,{bn-2}是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)设数列{nbn}的前n项和为Sn,求Sn的表达式;
(3)数列{cn}满足cn=an•(bn+2-2),求数列{cn}的最大项.
(1)求数列{an}和{bn}的通项公式;
(2)设数列{nbn}的前n项和为Sn,求Sn的表达式;
(3)数列{cn}满足cn=an•(bn+2-2),求数列{cn}的最大项.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:综合题,整体思想,等差数列与等比数列
分析:(1)根据数列的通项公式,递推的方法解决.
(2)利用错位相减的方法,转化为等比数列整体求解.
(3)利用相邻两项作商的方法,结合不等式判断最大项,并求出来.
(2)利用错位相减的方法,转化为等比数列整体求解.
(3)利用相邻两项作商的方法,结合不等式判断最大项,并求出来.
解答:
解:(1)依题意得:(a3-a2)-(a2-a1)=-1-(-2)=1.
所以an+1-an=(a2-a1)+(n-1)•1=n-3,
故当n≥2时,有an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(n-4)+(n-5)+…+(-1)+(-2)+6=
,
又因为n=1时,a1=6也适合上式,
所以an=
(n∈N*)
又∵
=
=
,b1-2=4,∴bn-2=4•(
)n-1=(
)n-3,
故bn=(
)n-3+2(n∈N*)
(2)Sn=b1+2b2+3b3+…+nbn
=[(
)-2+2]+2[(
)-1+2]+3[(
)0+2]+…+n[(
)n-3+2]
=[(
)-2+2(
)-1+3[(
)0+…+n(
)n-3]+2(1+2+3+…+n)
=[(
)-2+2(
)-1+3[(
)0+…+n(
)n-3]+n(1+n)
令S=(
)-2+2(
)-1+3[(
)0+…+n(
)n-3
则
S=(
)-1+2(
)0+3[(
)1+…+n(
)n-2
两式相减得:则
S=(
)-2+(
)-1+(
)0+…+(
)n-3-n(
)n-2
那么S=(
)-3+(
)-2+(
)-1+…+(
)n-4-n(
)n-3=
-n(
)n-3=16-8(n+2)(
)n
所以Sn=16-8(n+2)(
)n+n(n+1)
(3)cn=an•(bn+2-2)=
(n2-7n+18)•(
)n-1=(n2-7n+18)•(
)n
令
=
=
<1,
得n2-9n+24>0,
而n2-9n+24=(n-
)2+
>0显然对任意的正整数n都成立,
所以数列{cn}是单调递减数列,最大项是c1=6.
所以an+1-an=(a2-a1)+(n-1)•1=n-3,
故当n≥2时,有an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(n-4)+(n-5)+…+(-1)+(-2)+6=
| n2-7n+18 |
| 2 |
又因为n=1时,a1=6也适合上式,
所以an=
| n2-7n+18 |
| 2 |
又∵
| b2-2 |
| b1-2 |
| 2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故bn=(
| 1 |
| 2 |
(2)Sn=b1+2b2+3b3+…+nbn
=[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令S=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
两式相减得:则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
那么S=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2 |
所以Sn=16-8(n+2)(
| 1 |
| 2 |
(3)cn=an•(bn+2-2)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令
| cn+1 |
| cn |
[(n+1)2-7(n+1)+18]•(
| ||
(n2-7n+18)•(
|
| n2-5n+12 |
| 2(n2-7n+18) |
得n2-9n+24>0,
而n2-9n+24=(n-
| 9 |
| 2 |
| 15 |
| 4 |
所以数列{cn}是单调递减数列,最大项是c1=6.
点评:本题综合考察了数列的公式性质,求和的方法错位相减,作商判断最大项.对函数不等式的考察比较深刻.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知在二面角α-l-β的α面上有Rt△ABC,斜边BC在l上,A在β面上的射影为D,∠ABD为θ1,∠ACD为θ2,二面角α-l-β为θ.请问以下条件哪一个成立( )
| A、sin2θ=sin2θ1+sin2θ2 |
| B、cos2θ=cos2θ1+cos2θ2 |
| C、tan2θ=tan2θ1+tan2θ2 |
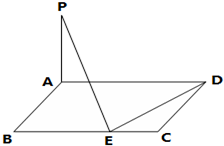 (理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.
(理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.