题目内容
设各项都是正整数的无穷数列{an}满足:对任意n∈N*,有an<an+1.记bn=aan.
(1)若数列{an}是首项a1=1,公比q=2的等比数列,求数列{bn}的通项公式;
(2)若bn=3n,证明:a1=2;
(3)若数列{an}的首项a1=1,cn=a an+1,{cn}是公差为1的等差数列.记dn=-2n•an,Sn=d1+d2+…+dn-1+dn,问:使Sn+n•2n+1>50成立的最小正整数n是否存在?并说明理由.
(1)若数列{an}是首项a1=1,公比q=2的等比数列,求数列{bn}的通项公式;
(2)若bn=3n,证明:a1=2;
(3)若数列{an}的首项a1=1,cn=a an+1,{cn}是公差为1的等差数列.记dn=-2n•an,Sn=d1+d2+…+dn-1+dn,问:使Sn+n•2n+1>50成立的最小正整数n是否存在?并说明理由.
考点:等差数列与等比数列的综合,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)利用等比数列的通项公式求出an=2n-1,再求数列{bn}的通项公式;
(2)根据反证法排除a1=1和a1≥3,即可证明:a1=2;
(3)首先{an}是公差为1的等差数列,an=n,再利用错位相减法,即可得出结论.
(2)根据反证法排除a1=1和a1≥3,即可证明:a1=2;
(3)首先{an}是公差为1的等差数列,an=n,再利用错位相减法,即可得出结论.
解答:
解:(1)∵数列{an}是首项a1=1,公比q=2的等比数列,
∴an=2n-1,
∴b1=aa1=a1=1,bn=aan=a2n-1=22n-1-1;
(2)根据反证法排除a1=1和a1≥3.
证明:假设a1≠2,∴a1=1和a1≥3
①当a1=1时,b1=aa1=a1=1与b1=3矛盾,∴a1≠1;
②当a1≥3时,即a1≥3=b1=aa1,又an<an+1,
∴a1≤1与a1≥3矛盾;
由①②可知a1=2.
(3)首先{an}是公差为1的等差数列,
证明如下:∵an<an+1,
∴n≥2时,an-1<an,
∴an≥an-1+1,
∴an≥am+(n-m)(m<n),
∴aan+1+1≥aan+1+[an+1+1-(an+1)]即cn+1-cn≥an+1-an,
由题设1≥an+1-an,
又an+1-an≥1,
∴an+1-an=1,
即{an}是等差数列.
又{an}的首项a1=1,
∴an=n,
∴Sn=-(2+2•22+3•23+…+n•2n),对此式两边乘以2,得2Sn=-22-2•23-3•24-…-n•2n+1
两式相减得Sn=2+22+23+…+2n-n•2n+1=2n+1-n•2n+1-2Sn+n•2n+1=2n+1-2,Sn+n•2n+1>50,
即2n+1≥52,
当n≥5时,2n+1=64>52,即存在最小正整数5使得Sn+n•2n+1>50成立.
∴an=2n-1,
∴b1=aa1=a1=1,bn=aan=a2n-1=22n-1-1;
(2)根据反证法排除a1=1和a1≥3.
证明:假设a1≠2,∴a1=1和a1≥3
①当a1=1时,b1=aa1=a1=1与b1=3矛盾,∴a1≠1;
②当a1≥3时,即a1≥3=b1=aa1,又an<an+1,
∴a1≤1与a1≥3矛盾;
由①②可知a1=2.
(3)首先{an}是公差为1的等差数列,
证明如下:∵an<an+1,
∴n≥2时,an-1<an,
∴an≥an-1+1,
∴an≥am+(n-m)(m<n),
∴aan+1+1≥aan+1+[an+1+1-(an+1)]即cn+1-cn≥an+1-an,
由题设1≥an+1-an,
又an+1-an≥1,
∴an+1-an=1,
即{an}是等差数列.
又{an}的首项a1=1,
∴an=n,
∴Sn=-(2+2•22+3•23+…+n•2n),对此式两边乘以2,得2Sn=-22-2•23-3•24-…-n•2n+1
两式相减得Sn=2+22+23+…+2n-n•2n+1=2n+1-n•2n+1-2Sn+n•2n+1=2n+1-2,Sn+n•2n+1>50,
即2n+1≥52,
当n≥5时,2n+1=64>52,即存在最小正整数5使得Sn+n•2n+1>50成立.
点评:数列的通项与求和,离不开等差数列与等比数列,掌握等差数列与等比数列的通项与求和是关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
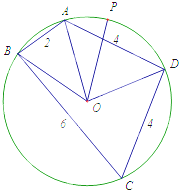 已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.
已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.