题目内容
设F1,F2分别为椭圆W:
+y2=1的左、右焦点,斜率为k的直线l经过右焦点F2,且与椭圆W相交于A,B两点.
(Ⅰ)求△ABF1的周长;
(Ⅱ)如果△ABF1为直角三角形,求直线l的斜率k.
| x2 |
| 2 |
(Ⅰ)求△ABF1的周长;
(Ⅱ)如果△ABF1为直角三角形,求直线l的斜率k.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆的定义,可求△ABF1的周长;
(Ⅱ)如果△ABF1为直角三角形,分类讨论,利用韦达定理,即可求直线l的斜率k.
(Ⅱ)如果△ABF1为直角三角形,分类讨论,利用韦达定理,即可求直线l的斜率k.
解答:
解:(Ⅰ)椭圆W的长半轴长a=
,左焦点F1(-1,0),右焦点F2(1,0),…(2分)
由椭圆的定义,得|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
所以△ABF1的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=4
.…(5分)
(Ⅱ)因为△ABF1为直角三角形,
所以∠BF1A=90°,或∠BAF1=90°,或∠ABF1=90°,
当∠BF1A=90°时,
设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2),…(6分)
由y=k(x-1),代入椭圆方程可得 (1+2k2)x2-4k2x+2k2-2=0,…(7分)
所以x1+x2=
,x1x2=
.…(8分)
由∠BAF1=90°,得
•
=0,…(9分)
因为
=(x1+1,y1),
=(x2+1,y2),
所以
•
=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2=0,…(10分)
解得k=±
.…(11分)
当∠ABF1=90°时,
则点A在以线段F1F2为直径的圆x2+y2=1上,也在椭圆W上,
由
解得A(0,1),或(0,-1),…(13分)
根据两点间斜率公式,得k=±1,
综上,直线l的斜率k=±
,或k=±1时,△ABF1为直角三角形.…(14分)
| 2 |
由椭圆的定义,得|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
所以△ABF1的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=4
| 2 |
(Ⅱ)因为△ABF1为直角三角形,
所以∠BF1A=90°,或∠BAF1=90°,或∠ABF1=90°,
当∠BF1A=90°时,
设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2),…(6分)
由y=k(x-1),代入椭圆方程可得 (1+2k2)x2-4k2x+2k2-2=0,…(7分)
所以x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
由∠BAF1=90°,得
| F1A |
| F1B |
因为
| F1A |
| F1B |
所以
| F1A |
| F1B |
解得k=±
| ||
| 7 |
当∠ABF1=90°时,
则点A在以线段F1F2为直径的圆x2+y2=1上,也在椭圆W上,
由
|
根据两点间斜率公式,得k=±1,
综上,直线l的斜率k=±
| ||
| 7 |
点评:椭圆的定义是解决椭圆问题的常用方法,直线与椭圆联立,利用韦达定理是解决直线与椭圆位置关系问题的方法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
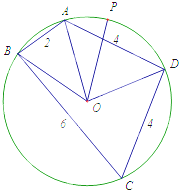 已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.
已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4. 某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了n人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了n人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示: