题目内容
从5名男生,3名女生中选4名代表,至少有1名女生的选法有多少种?
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:从5名男生,3名女生中选4名代表,共有C83种结果,其中包括不合题意的没有女生的选法,其中没有女生的选法有C54用所有的结果是减去不合题意的数字,得到结果.
解答:
解:从5名男生,3名女生中选4名代表,共有C84种结果,其中包括不合题意的没有女生的选法,
其中没有女生的选法有C54
∴至少有1名女生的选法有C84-C54=70-5=65.
其中没有女生的选法有C54
∴至少有1名女生的选法有C84-C54=70-5=65.
点评:本题考查排列组合简单的计数原理的应用,利用间接法,比较简单.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,且cosA=
,则sin2
+cos2A的值为( )
| 1 |
| 3 |
| B+C |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
y=ax2+bx+c(a≠0)的图象如图所示,则点M(a,bc)在( )
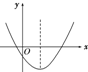

| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
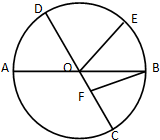 如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若
如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若