题目内容
数列前n项和为n3，且前n个偶数项的和为n2（4n+3），则前n个奇数项的和为（ ）
| A、-3n2（n+1） | ||
| B、n2（4n-3） | ||
| C、-3n2 | ||
D、
|
考点：数列的求和
专题：等差数列与等比数列
分析：数列前n项和为n3，可得前2n项的和为8n3，又前n个偶数项的和为n2（4n+3），即可得出前n个奇数项的和=8n3-n2（4n+3）．
解答：
解：∵数列前n项和为n3，
∴前2n项的和为8n3，
又前n个偶数项的和为n2（4n+3），
∴前n个奇数项的和=8n3-n2（4n+3）=n2（4n-3），
故选：B．
∴前2n项的和为8n3，
又前n个偶数项的和为n2（4n+3），
∴前n个奇数项的和=8n3-n2（4n+3）=n2（4n-3），
故选：B．
点评：本题考查了数列的前n项和的求法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图，圆锥SO中，AB、CD为底面圆的两条直径，AB∩CD=0，且AB⊥CD，SO=OB=2，P为SB的中点．异面直线SA与PD所成角的正切值为（ ）在△ABC中，角A、B、C所对的边分别为a，b，c，且cosA=
，则sin2
+cos2A的值为（ ）
| 1 |
| 3 |
| B+C |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
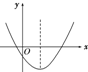
y=ax2+bx+c（a≠0）的图象如图所示，则点M（a，bc）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |