题目内容
已知ln(
)=2ax,求a的值.
| e-3x+1 |
| e3x+1 |
考点:对数的运算性质
专题:函数的性质及应用
分析:由已知得ln(
)=lne-3x=-3x=2ax,由此能求出a=-
.
| e-3x+1 |
| e3x+1 |
| 3 |
| 2 |
解答:
解:∵ln(
)=2ax,
ln(
)=ln(
)
=lne-3x=-3x=2ax,
解得a=-
.
| e-3x+1 |
| e3x+1 |
ln(
| e-3x+1 |
| e3x+1 |
| ||
| e3x+1 |
=lne-3x=-3x=2ax,
解得a=-
| 3 |
| 2 |
点评:本题考查实数值的求法,是基础题,解题时要注意对数、指数的性质和运算法则的合理运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
若对于任何实数,二次不等式ax2-x+c<0的解集为R,那么a、c应满足( )
A、a>0且ac≤
| ||
B、a<0且ac<
| ||
C、a<0且ac>
| ||
| D、a<0且ac<0 |
y=ax2+bx+c(a≠0)的图象如图所示,则点M(a,bc)在( )
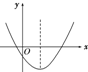

| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
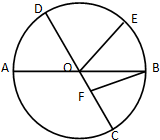 如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若
如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=0,且AB⊥CD,SO=OB=2,P为SB的中点.异面直线SA与PD所成角的正切值为( )