题目内容
已知函数f(x)=x2+bx+c和g(x)=2x+b,若对任意的x∈R,恒有f(x)≥g(x)
(1)证明:c≥1且c≥b
(2)证明:当x≥0时,(x+c)2≥f(x)
(1)证明:c≥1且c≥b
(2)证明:当x≥0时,(x+c)2≥f(x)
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据对任意的x∈R,恒有f(x)≥g(x),可得x2+(b-2)x+c-b≥0恒成立,即△=(b-2)2-4(c-b)≤0,进而分别判断c-1和c-b的符号,可得结论;
(2)结合(1)中结论,可得2c-b=c+(c-b)≥0,c(c+1)≥0,利用做差法可得:(x+c)2-f(x)=(2c-b)x+c(c-1),再由一次函数的图象和性质,可得结论.
(2)结合(1)中结论,可得2c-b=c+(c-b)≥0,c(c+1)≥0,利用做差法可得:(x+c)2-f(x)=(2c-b)x+c(c-1),再由一次函数的图象和性质,可得结论.
解答:
证明:(1)∵对任意的x∈R,恒有f(x)≥g(x),f(x)=x2+bx+c,g(x)=2x+b,
∴x2+(b-2)x+c-b≥0恒成立
所以△=(b-2)2-4(c-b)≤0,从而 c≥
+1
于是 c-1≥
≥0,
c-b≥
+1-b=(
-1)2≥0
所以 c≥1且c≥b;
(2)∵(x+c)2-f(x)=(2c-b)x+c(c-1)
当x≥0时,由(1)2c-b=c+(c-b)≥0,
c(c+1)≥0
∴(x+c)2-f(x)=(2c-b)x+c(c-1)≥0
故:当x≥0时,(x+c)2≥f(x)
∴x2+(b-2)x+c-b≥0恒成立
所以△=(b-2)2-4(c-b)≤0,从而 c≥
| b2 |
| 4 |
于是 c-1≥
| b2 |
| 4 |
c-b≥
| b2 |
| 4 |
| b |
| 2 |
所以 c≥1且c≥b;
(2)∵(x+c)2-f(x)=(2c-b)x+c(c-1)
当x≥0时,由(1)2c-b=c+(c-b)≥0,
c(c+1)≥0
∴(x+c)2-f(x)=(2c-b)x+c(c-1)≥0
故:当x≥0时,(x+c)2≥f(x)
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
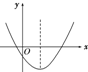
y=ax2+bx+c(a≠0)的图象如图所示,则点M(a,bc)在( )

| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
非零向量
,
满足
•
-2
2
2=0,|
|+|
|=1,则
与
的夹角的最小值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|