题目内容
设集合A={x||x|＜2}，若B⊆A，则集合B可以是（ ）
| A、{x|-1＜x＜0} |
| B、{x|-1＜x＜3} |
| C、{x|-3＜x＜2} |
| D、{x|-3＜x＜3} |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：化简集合A={x|-2＜x＜2}，从而可知，{x|-1＜x＜0}⊆{x|-2＜x＜2}．
解答：
解：集合A={x||x|＜2}={x|-2＜x＜2}，
则{x|-1＜x＜0}⊆{x|-2＜x＜2}，
故A正确．
故选A．
则{x|-1＜x＜0}⊆{x|-2＜x＜2}，
故A正确．
故选A．
点评：本题考查了集合的化简与集合的包含关系的应用，属于基础题．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
不等式|y|≤x表示的平面区域为（ ）
A、 |
B、 |
C、 |
D、 |
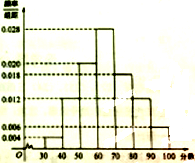某校高一年级共有800名学生，其中男生480名，女生320名，在某次满分为100分的数学考试中，所有学生成绩在30分及30分以上，成绩在“80分及80分以上”的学生视为优秀，现按性别采用分层抽样的方法抽取100名学生，将他们的成绩按[30，40）、[40，50）、[50，60）、[60，70）、[70，80）、[80，90）、[90，100）分成七组，得到的频率分布直方图如图所示：已知函数y=2f′(x)的图象如图所示，则函数f（x）的单调递增区间为（ ）
| A、（-∞，0）和（2，+∞） |
| B、（0，2） |
| C、（-∞，0）∪（2，+∞） |
| D、（-∞，1） |
