题目内容
已知sinα+sinβ=
,cosα+cosβ=
,求cos(α-β)和cos(α+β).
| 1 |
| 4 |
| 1 |
| 3 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由题意,把sinα+sinβ=
与cosα+cosβ=
分别平方,两式相加,求出cos(α-β)的值,两式相减,求出cos(α+β)的值.
| 1 |
| 4 |
| 1 |
| 3 |
解答:
解:∵sinα+sinβ=
,cosα+cosβ=
,
∴sin2α+2sinαsinβ+sin2β=
①,
cos2α+2cosαcosβ+cos2β=
②;
∴①+②得,1+2(sinαsinβ+cosαcosβ)+1=
+
,
即2cos(α-β)=-
,
∴cos(α-β)=-
;
②-①得,(cos2α-sin2α)+(cos2β-sin2β)+2(cosαcosβ-sinαsinβ)=
,
即cos2α+cos2β+2cos(α+β)=
,
∴2cos(α+β)cos(α-β)+2cos(α+β)=
,
∴2cos(α+β)=
×
=
,
∴cos(α+β)=
;
综上,cos(α-β)=-
、cos(α+β)=
.
| 1 |
| 4 |
| 1 |
| 3 |
∴sin2α+2sinαsinβ+sin2β=
| 1 |
| 16 |
cos2α+2cosαcosβ+cos2β=
| 1 |
| 9 |
∴①+②得,1+2(sinαsinβ+cosαcosβ)+1=
| 1 |
| 16 |
| 1 |
| 9 |
即2cos(α-β)=-
| 263 |
| 144 |
∴cos(α-β)=-
| 263 |
| 288 |
②-①得,(cos2α-sin2α)+(cos2β-sin2β)+2(cosαcosβ-sinαsinβ)=
| 7 |
| 144 |
即cos2α+cos2β+2cos(α+β)=
| 7 |
| 144 |
∴2cos(α+β)cos(α-β)+2cos(α+β)=
| 7 |
| 144 |
∴2cos(α+β)=
| 7 |
| 144 |
| 1 | ||
1-
|
| 14 |
| 25 |
∴cos(α+β)=
| 7 |
| 25 |
综上,cos(α-β)=-
| 263 |
| 288 |
| 7 |
| 25 |
点评:本题考查了三角函数的恒等变换问题,解题时应灵活应用公式进行计算,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x3-x-3=0的实数解所在的区间是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
以(-4,0)、(4,0)为焦点,2a=4的双曲线的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
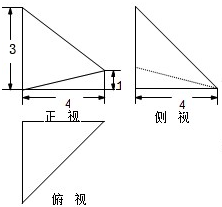 已知一个几何体的三视图如图所示,其中正视图是直角梯形.
已知一个几何体的三视图如图所示,其中正视图是直角梯形.