题目内容

已知棱台的上，下底面积分别为9cm2，16cm2，则它的中截面积为
 
．
考点：棱台的结构特征
专题：空间位置关系与距离
分析：分别设出棱台和上部小棱锥的高2r，a，结合已知由相似比定理得到(
a
a+2r
)2=
9
16
，由此得到a与r的关系，进一步由相似比定理得答案．
解答： 解：如图，

不妨设棱台高为2r，上部分小棱锥的高为a，
则(
a
a+2r
)2=
9
16
，
∴
a
a+2r
=
3
4
，a=6r，
又(
a
a+r
)2=
S上
S中
，
∴
9
S中
=(
6r
7r
)2=
36
49
，
∴中截面积为S中=
49
4
．
故答案为：
49
4
．
点评：本题考查了棱台的结构特征，关键是明确相似多边形的面积比等于相似比的平方，是中档题．
练习册系列答案
相关题目
已知sinα+sinβ=
1
4
，cosα+cosβ=
1
3
，求cos（α-β）和cos（α+β）．
已知二次函数f（x）与x轴的两个交点为（-2，0），（1，0）且最大值为
9
2
，则f（x）=
 
．
利用单位圆分别写出满足下列条件的角的集合：
（1）sinα＞-
1
2
；
（2）cosα＞
1
2
；
（3）tanα＞1．
已知y2+2lny=x4，且函数y=y（x），求
dy
dx
．
在△DEF中，|
DE
|=1，|
DF
|=2，
EP
=-2
FP
，
DP
•
FP
=-
8
9
，则∠EDF=
 
．
已知二次函数f（x）=ax2+x．对于?x∈[0，1]，f（x）≤1成立，试求实数a的取值范围．
f（x）≤1?ax2+x≤1，x∈[0，1]…①
当x=0时，a≠0，①式显然成立；
当x∈（0，1]时，①式化为a≤
1
x2
-
1
x
在x∈（0，1]上恒成立．
设t=
1
x
，则t∈[1，+∞），则有a≤t2-t，所以只须a≤（t2-t）min=0
⇒a≤0，又a≠0，故a＜0
综上，所求实数a的取值范围是
 
．
函数y=esinx（-π≤x≤π）的大致图象为（　　）
A、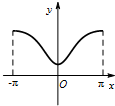
B、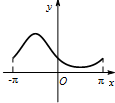
C、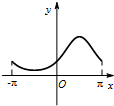
D、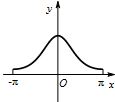
已知曲线C的极坐标方程ρ=2sinθ，直线l的参数方程
x=3+
2
2
t
y=
2
2
t
（t为参数），以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系；
（1）求曲线C与直线l的直角坐标方程．
（2）若M、N分别为曲线C与直线l上的两个动点，求|MN|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网