题目内容
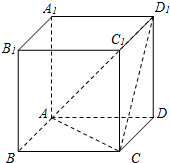 在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是
在如图所示的棱长为2的正方体ABCD-A1B1C1D1中,作与平面ACD1平行的截面,则截得的三角形中面积最大的值是考点:棱柱的结构特征
专题:空间位置关系与距离
分析:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,结合图形判断截面为正六边形时,截面的面积最大,利用梯形的面积公式计算可得最大面积.
解答:
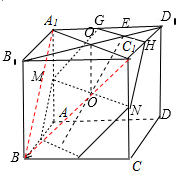 解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,
解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,
∵正方体ABCD-A1B1C1D1的棱长为2,
∴A1C1=C1B=A1B=2
,
∴S△A1C1B=
×2
×
×2
=2
,
如图平面α截正方体所得截面为正六边形,此时,截面面积最大,其中MN=2
,GH=
,OE=
=
,
截面面积S=2×
×OE=3
.
故答案为:2
,3
.
 解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,
解:截得的三角形中面积最大是以正方体的表面正方形的对角线所构成的等边三角形,如图中的△A1C1B,∵正方体ABCD-A1B1C1D1的棱长为2,
∴A1C1=C1B=A1B=2
| 2 |
∴S△A1C1B=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 3 |
如图平面α截正方体所得截面为正六边形,此时,截面面积最大,其中MN=2
| 2 |
| 2 |
1+
|
| ||
| 2 |
截面面积S=2×
| ||||
| 2 |
| 3 |
故答案为:2
| 3 |
| 3 |
点评:本题考查了正方体的截面图形的面积计算,关键是判断截面的形状,根据形状计算面积.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
若平面向量
,
满足|2
-
|≤3,则
•
的范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(-
|
已知函数f(x)满足f(x+2)=f(x-2),y=f(x-2)关于y轴对称,当x∈(0,2)时,f(x)=log2x2,则下列结论中正确的是( )
| A、f(4.5)<f(7)<f(6.5) |
| B、f(7)<f(4.5)<f(6.5) |
| C、f(7)<f(6.5)<f(4.5) |
| D、f(4.5)<f(6.5)<f(7) |
函数f(x)=ex-
的零点所在的区间是( )
| 1 |
| x |
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|