题目内容
8.已知x,y满足$\left\{\begin{array}{l}x+2y-3≤0\\ x+3y-3≥0\\ y≤1\end{array}\right.$,z=2x+y的最大值是m,若正数a,b满足a+b=m,则$\frac{1}{a}+\frac{4}{b}$的最小值为$\frac{3}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合进行求解,得大m的值,然后利用1的代换,结合基本不等式的性质进行求解即可.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,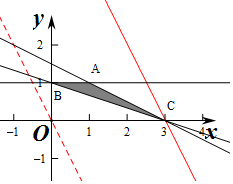
由图象可知当直线y=-2x+z经过点C时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{x+2y-3=0}\\{x+3y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,即C(3,0),
代入目标函数z=2x+y得z=2×3+0=6.
即目标函数z=2x+y的最大值为6.
即m=6,
则a+b=6,即$\frac{a+b}{6}$=1,
则$\frac{1}{a}+\frac{4}{b}$=($\frac{1}{a}+\frac{4}{b}$)×$\frac{a+b}{6}$=$\frac{1}{6}$(1+4+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{1}{6}$(5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$)=$\frac{5+4}{6}$=$\frac{3}{2}$,
当且仅当$\frac{b}{a}$=$\frac{4a}{b}$,即b2=4a2,即b=2a时取等号,
故答案为:$\frac{3}{2}$
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想以及利用基本不等式的性质是解决此类问题的基本方法.

练习册系列答案
相关题目
18.某香料加工厂生产“沉鱼落雁”和“国色天香”两种香料,已知生产两种香料每吨所需的原材料A,B,C的数量和一周内可用资源数量如下表所示:
如果“沉鱼落雁”每吨的利润为400元,“国色天香”每吨的利润为300元,那么应如何安排生产,才能使香料加工厂每周的利润最大?并求出最大利润.
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
19.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=x2+1 | B. | y=3-2x | C. | $y=\frac{1}{x}$ | D. | y=-x2+1 |
17.下列函数中是偶函数,且在(1,+∞)上是单调递减的函数为( )
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |
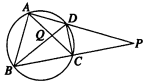 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )