题目内容
11．复数z=$\frac{1+i}{i}$，$\overline z$是它的共轭复数，则$z•\overline z$=2．分析 利用复数的运算法则、共轭复数的定义即可得出．
解答 解：z=$\frac{1+i}{i}$=$\frac{-i（1+i）}{-i•i}$=1-i，则$z•\overline z$=（1-i）（1+i）=2．
故答案为：2．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．当0＜a＜1时，函数y=loga（x2-4x+3）的单调增区间为（ ）
| A． | （-∞，2] | B． | [2，+∞） | C． | （-∞，1） | D． | （3，+∞） |
19．下列函数中，在区间（0，+∞）上是增函数的是（ ）
| A． | y=x2+1 | B． | y=3-2x | C． | $y=\frac{1}{x}$ | D． | y=-x2+1 |
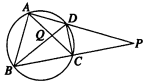如图所示，圆内接四边形ABCD的一组对边AD，BC的延长线相交于点P，对角线AC，BD相交于点Q，则图中相似三角形共有（ ）