题目内容
5.下列函数中,在(-∞,0)内为减函数的是( )| A. | y=3x | B. | y=x3 | C. | y=2x+1 | D. | y=x2+1 |
分析 根据基本初等函数的图象与性质,对选项中的函数单调性判断即可.
解答 解:对于A,函数y=3x,在(-∞,+∞)内是单调增函数,不合题意;
对于B,函数y=x3,在(-∞,+∞)内是单调增函数,不合题意;
对于C,函数y=2x+1,在(-∞,+∞)内是单调增函数,不合题意;
对于D,函数y=x2,是二次函数,图象是抛物线,对称轴为x=0,
且在(-∞,0)内是单调减函数,满足题意.
故选:D.
点评 本题考查了基本初等函数的单调性问题,是基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
15.在平面直角坐标系中,“直线ax+y-1=0与直线x+ay+2=0平行”是“a=1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
17.下列函数中是偶函数,且在(1,+∞)上是单调递减的函数为( )
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |
14.若正实数x,y满足log2(x+3y)=log4x2+log2(2y),则3x+y的最小值是( )
| A. | 12 | B. | 6 | C. | 16 | D. | 8 |
15.在△ABC中,a、b、c分别是角A、B、C的对边,若角A、B、C依次成等差数列,且-x2+5x-4>0的解集为{x|a<x<c},则S△ABC=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
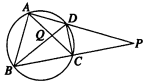 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )