题目内容
10.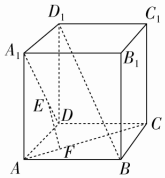 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )| A. | EF至多与A1D、AC之一垂直 | B. | EF与A1D、AC都垂直 | ||
| C. | EF与BD1相交 | D. | EF与BD1异面 |
分析 连接D1E,BF,根据A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,判断D1E,BF交与同一点M,再根据成比例线段证明EF∥D1B,由D1B⊥AC,D1B⊥A1D证明EF与A1D、AC都垂直.
解答 解:如图所示;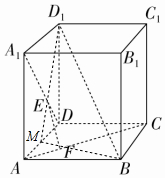
连接D1E,与AD交与M点处,因为A1E=$\frac{2}{3}$A1D,所以DM=$\frac{1}{2}$A1D1=$\frac{1}{2}$AD,
所以M为AD中点,
连接BF,交AD与N点,因为AF=$\frac{1}{3}$AC,所以AN=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
所以N为AD中点,
所以M,N重合;且$\frac{ME}{{ED}_{1}}$=$\frac{MF}{FB}$=$\frac{1}{2}$,所以EF∥D1B,
又AC⊥平面DD1B,所以AC⊥BD1,
所以AC⊥EF,
同理,A1D⊥EF,
所以EF与A1D、AC都垂直,且相交,
∴B正确,A、EF至多与A1D、AC之一垂直错误,
C、EF与BD1相交错误,D、EF与BD1异面错误.
故选:B.
点评 本题考查了立体几何中线线平行与垂直的判断问题,是综合性问题.

练习册系列答案
相关题目
18.某香料加工厂生产“沉鱼落雁”和“国色天香”两种香料,已知生产两种香料每吨所需的原材料A,B,C的数量和一周内可用资源数量如下表所示:
如果“沉鱼落雁”每吨的利润为400元,“国色天香”每吨的利润为300元,那么应如何安排生产,才能使香料加工厂每周的利润最大?并求出最大利润.
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
5.与函数f(x)=2x的图象关于直线y=x对称的曲线C对应的函数为g(x),则函数$y=g({\frac{1}{x}})•g({4x})({\frac{1}{8}≤x≤4})$的值域为[-8,1].
15.在平面直角坐标系中,“直线ax+y-1=0与直线x+ay+2=0平行”是“a=1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
2.当0<a<1时,函数y=loga(x2-4x+3)的单调增区间为( )
| A. | (-∞,2] | B. | [2,+∞) | C. | (-∞,1) | D. | (3,+∞) |
19.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=x2+1 | B. | y=3-2x | C. | $y=\frac{1}{x}$ | D. | y=-x2+1 |
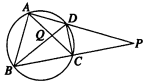 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )