题目内容
已知三棱锥的三条侧棱两两垂直，且各侧棱长都等于a，底面为正三角形
（1）若三棱锥的全面积为3+
，求a的值；
（2）若该三棱锥的外接球的表面积为3π，求a的值．
（1）若三棱锥的全面积为3+
| 3 |
（2）若该三棱锥的外接球的表面积为3π，求a的值．
考点：棱柱、棱锥、棱台的侧面积和表面积,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：（1）根据几何性质，列方程：
+
a2=3+
，（2）把三棱锥镶嵌在正方体中，棱长为a，求出体对角线
a，运用2R=
a求出半径即可得到答案．
| 3a2 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
解答：
解：（1）∵三棱锥的三条侧棱两两垂直，且各侧棱长都等于a，底面为正三角形
∴底面边长为
a，
∴三棱锥的全面积为：
+
a2，
∵全面积为3+
，
∴a2=2，a=
，
（2）三棱锥的外接球的半径为R，
∵把三棱锥镶嵌在正方体中，棱长为a，
∴体对角线
a，
∴2R=
a，
∵外接球的表面积为3π
∴R=
，
∴2×
=
a，a=1
故a的值为1．
∴底面边长为
| 2 |
∴三棱锥的全面积为：
| 3a2 |
| 2 |
| ||
| 2 |
∵全面积为3+
| 3 |
∴a2=2，a=
| 2 |
（2）三棱锥的外接球的半径为R，
∵把三棱锥镶嵌在正方体中，棱长为a，
∴体对角线
| 3 |
∴2R=
| 3 |
∵外接球的表面积为3π
∴R=
| ||
| 2 |
∴2×
| ||
| 2 |
| 3 |
故a的值为1．
点评：本题考查了几何体的性质，运用求解表面积，属于中档题．
练习册系列答案
相关题目
盒中有4个相同的球，标号1，2，3，4．现从盒中随机摸一个，若摸出球上的数字是被摸球中最大的则留下，否则放回，则5次内（包括5次）把球摸完的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
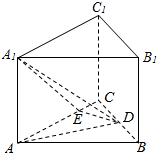如图，在正三棱柱ABC-A1B1C1中，AB=4，AA1=| 7 |
（1）证明：平面A1DE⊥平面ACC1A1；
（2）求直线AD和平面A1DE所成角的正弦值．
空间4点A，B，C，D共面但不共线，下列结论中正确的是（ ）
| A、4点中必能找出其中3点共线 |
| B、4点中必能找出其中3点不共线 |
| C、AB，BC，CD，DA中必有两条平行 |
| D、AB与CD必相交 |