题目内容
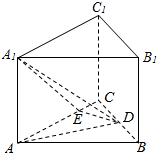 如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=
如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=| 7 |
(1)证明:平面A1DE⊥平面ACC1A1;
(2)求直线AD和平面A1DE所成角的正弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)欲证平面A1DE⊥平面ACC1A1,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACC1A1垂直,而根据DE⊥AA1而DE⊥AE.AA1∩AE=A满足线面垂直的判定定理可知DE⊥平面ACC1A1;
(2)过点A做AF垂直A1E于F,连接DF,由(1)知:平面A1DE⊥平面ACC1A1.所以AF⊥平面A1DE,则∠ADF即为直线AD和平面A1DE所成角,在三角形ADF中求出此角即可.
(2)过点A做AF垂直A1E于F,连接DF,由(1)知:平面A1DE⊥平面ACC1A1.所以AF⊥平面A1DE,则∠ADF即为直线AD和平面A1DE所成角,在三角形ADF中求出此角即可.
解答:
解:(1)如图所示,由正三棱柱ABC-A1B1C1的性质知AA1⊥平面A1B1C1
又DE?平面A1B1C1,
所以DE⊥AA1.
而DE⊥AE.AA1∩AE=A,
所以DE⊥平面ACC1A1,
又DE?平面A1DE,
故平面A1DE⊥平面ACC1A1.
(2)过点A做AF垂直A1E于F,连接DF,

由(1)知:平面A1DE⊥平面ACC1A1.
所以AF⊥平面A1DE,
则∠ADF即为直线AD和平面A1DE所成角,
因为DE⊥平面ACC1A1.
所以DE⊥AC,
而△ABC是边长为4的正三角形,
所以AD=2
,AE=4-CE=4-
CD=3,
又因为AA1=
,
所以A1E=
=
=4,
AF=
=
,
所以sin∠ADF=
=
,
故直线AD和平面A1DE所成角的正弦值为
又DE?平面A1B1C1,
所以DE⊥AA1.
而DE⊥AE.AA1∩AE=A,
所以DE⊥平面ACC1A1,
又DE?平面A1DE,
故平面A1DE⊥平面ACC1A1.
(2)过点A做AF垂直A1E于F,连接DF,

由(1)知:平面A1DE⊥平面ACC1A1.
所以AF⊥平面A1DE,
则∠ADF即为直线AD和平面A1DE所成角,
因为DE⊥平面ACC1A1.
所以DE⊥AC,
而△ABC是边长为4的正三角形,
所以AD=2
| 3 |
| 1 |
| 2 |
又因为AA1=
| 7 |
所以A1E=
| AA12+AE2 |
(
|
AF=
| AE•AA1 |
| A1E |
3
| ||
| 4 |
所以sin∠ADF=
| AF |
| AD |
| ||
| 8 |
故直线AD和平面A1DE所成角的正弦值为
| ||
| 8 |
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定及线面所成角的计算,考查逻辑思维能力、运算能力和推理论证能力,考查转化思想,属于基础题.

练习册系列答案
相关题目
函数f(x)=(m2-3)x m2-4m+3是幂函数,且在(0,+∞)上是减函数,则m=( )
| A、2 | B、-2 | C、2或-2 | D、4 |
若x,y满足
,则x+2y的最大值为( )
|
A、
| ||
| B、6 | ||
| C、11 | ||
| D、10 |
设点P是函数y=-
图象上的任意一点,点Q(2a,a-3)(a∈R),则|PQ|的最小值为( )
| 4-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|