题目内容
若数列{an}的通项an=n2-2λn(n属于正整数){an}为递增数列是真命题,求λ的范围.
考点:数列的函数特性
专题:点列、递归数列与数学归纳法
分析:由于{an}为递增数列是真命题,可得an+1>an.化简整理即可得出.
解答:
解:∵{an}为递增数列是真命题,
∴an+1>an.
∴(n+1)2-2λ(n+1)>n2-2λn,
化为λ<
对于?n∈N*恒成立.
∴λ<
.
∴λ的取值范围是(-∞,
).
∴an+1>an.
∴(n+1)2-2λ(n+1)>n2-2λn,
化为λ<
| 2n+1 |
| 2 |
∴λ<
| 3 |
| 2 |
∴λ的取值范围是(-∞,
| 3 |
| 2 |
点评:本题考查了数列的单调性、分离参数法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=log3(2x2-8x+m)的定义域为R,则m的取值范围是( )
| A、(8,+∞) |
| B、(-∞,8] |
| C、[8,+∞) |
| D、(-∞,8) |
 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,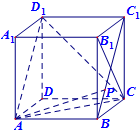 如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:
如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题: